双模型框架概述 [page::0][page::1]

• Model A（Poincaré–Mahalanobis）基于吸引子几何结构，强调基线系统稳定性。

- Model B（Correlation–Integral与Fibonacci诊断）聚焦波动簇和极端事件的多时间尺度检测。

• 两者结合提供了稳定性与尾部风险的互补视角。

Model A几何稳定性建模 [page::3][page::5][page::6]

• 利用洛伦兹系统轨迹的Poincaré截面与Mahalanobis距离评估参数。

- 后验聚集于标准参数(σ=10，ρ=28，β=8/3)，显示出稳定且收敛的马尔可夫链迹线。

Model B波动聚集与极端事件检测 [page::4][page::6]

• 基于相关积分及Fibonacci滚动窗口，捕捉多尺度波动簇。

- 诊断指标$D$-trace揭示事件簇的动态，短轨迹段突出显示极端波动区间。

模型跨系统泛化和比较分析 [page::6][page::7]

• Model A保持对洛伦兹吸引子的几何稳定锚定。

- Model B适用于罗斯勒吸引子，识别螺旋波动簇并用Fibonacci指标诊断极端事件。

• 传统固定窗口法对短期波动簇检测效果较差，Fibonacci窗口方法更优。

量化风险诊断方法优势 [page::7][page::8][page::12]

| 方法 | 优势 | 局限 |
|--------------|------------------------------|----------------------------------|
| 固定窗口滚动波动率 | 长期波动趋势捕捉 | 短期极端事件模糊 |
| Model A | 稳定性几何结构准确恢复 | 对尾部极端事件敏感度较低 |
| Model B | 多尺度波动聚集及稀有事件灵敏检测 | 计算复杂度较高 |

研究贡献与应用场景 [page::9][page::10]

• 建立了将混沌动力学几何结构与贝叶斯推断融合的风险建模理论。

- 适用于金融极端事件、系统性风险管理，亦可推广至气候、流行病和基础设施脆弱性研究。

• 为未来高维系统建模及代理模型集成提供理论和算法基础。

研究报告深度解读报告

报告题目：Chaotic Bayesian Inference: Strange Attractors as Risk Models for Black Swan Events
作者：Crystal Rust
发布机构与时间：不明确（推断为独立或学术发表，日期2025年9月11日）
主题领域：金融风险管理、黑天鹅事件、混沌动力学与贝叶斯推断交叉领域

---

一、元数据与报告概览

该报告提出了一种创新的风险建模框架，核心在于利用混沌吸引子（chaotic attractors）来定义贝叶斯推断中后验分布的几何结构。主要思路是通过结合厚尾先验（fat-tailed priors）与经典混沌系统（Lorenz和Rössler吸引子）动力学，来实现对内生波动簇集、幂律尾部和极端事件的自然生成和识别，从而为Taleb的黑天鹅及反脆弱理论提供结构性的数学解释与实现。

报告实现两个模型：

• Model A： Lorenz吸引子几何下的Poincaré–Mahalanobis距离模型，侧重几何稳定性；

- Model B： 基于Correlation Integral与Fibonacci诊断的模型，侧重波动簇集与极端事件的统计聚集。

这两个模型提供了对金融时间序列“风格化特征”（volatility clustering、fat tails、极端事件等）的再现能力，并提出了新型的压力测试与系统性风险诊断工具。最终，该框架搭起了统计厚尾不确定性与非线性混沌动力学之间的桥梁，并为未来基于数据的标定及与代理模型的融合指明方向。[page::0,1]

---

二、逐章节剖析

1. 引言与理论背景

传统金融风险模型多基于高斯假设及GARCH波动模型，系统低估极端事件概率。Taleb黑天鹅理论强调极端事件的本质非孤立异常，而是复杂系统内在不稳定性的产物。报告提出方法将后验分布配置于Lorenz或Rössler吸引子几何空间，并以厚尾先验为基础，实现波动簇集与极端事件的自发生成，从动力学结构中获得概率空间的厚尾特征。[page::1]

2. 相关研究（Condensed）

报告简要回顾黑天鹅理论（Taleb）、极值理论（EVT）、GARCH及粗糙波动模型、以及混沌在金融中的应用。其核心贡献在于将混沌直接嵌入概率风险架构中的贝叶斯推断，实现统计厚尾与动力几何的结合。这突破了传统模型仅通过参数化处理极端风险的局限。[page::2]

3. 方法论

3.1 建模动机

混沌系统可以双向分析：

• 若强调几何不变量，捕捉吸引子结构（Model A）

- 若强调统计递归与波动簇集，捕捉极端事件统计特征（Model B）

二者互补，构造双模型框架。厚尾先验（如Student-t分布）用于参数的不确定性表达，以保证模型对奇异大事件的敏感性。[page::2-3]

3.2 Model A - Poincaré–Mahalanobis方法

利用Lorenz轨迹在特定超平面的Poincaré截面形成的点集$\{z_i\}$，通过计算每个拟合参数$\theta$生成的模拟点与观测点集的Mahalanobis距离分布，然后通过Metropolis–Hastings采样构建后验分布。该方法基于吸引子几何稳定性，对参数空间的估计更加关注“形状匹配”，对异常点稳健，保持对系统基础结构的忠实表达。[page::3]

3.3 Model B - Correlation Integral与Fibonacci诊断

该模型关注轨迹的统计递归特性，计算吸引子点对的相关积分函数$C(r)$，通过小尺度内相关维度推断吸引子的复杂性。同时引入基于递归Fibonacci时间窗口（21、34、55、89步）计算的多尺度滞后中位数和MAD滤波，用于检测多时尺度的波动暴发（burst）。通过ABC-MCMC方法建立指标空间的距离，综合波动密度和Jaccard重叠，捕捉尾部事件聚集特征。此方法强调波动性簇集而非几何一致性。[page::4]

3.4 实验设计与实现细节

• 采用Metropolis–Hastings MCMC，迭代500步，采用自适应步长。

- 实验设定两个方案：（1）Lorenz–Lorenz：同一吸引子分别用模型A和B；（2）Lorenz–Rössler：模型A用于Lorenz，模型B用于Rössler，以测试跨吸引子的泛化能力。

• 诊断工具包含后验云、采样轨迹、吸引子重构、短轨道突出显示和$D$-trace系列等。[page::5]

---

4. 实验结果详解

4.1 Lorenz–Lorenz：同一系统不同模型比较

• 模型A成功重建Lorenz吸引子蝴蝶形截面点集，且参数Posterior云聚集于经典值$(\sigma=10, \rho=28, \beta=\frac{8}{3})$，采样链轨迹稳定且混合良好。表明其基于几何不变量的推断精确且稳定（见图1a-c）。

- 模型B强烈捕获波动簇集现象。短轨道强调（波动暴发区域）和$D$-trace实证显示对波动异常的敏感性。吸引子的重构图表明显，参数估计对突发事件更敏感，产生与模型A截然不同的后验分布重点（见图2a-c）。

两模型在相同系统上展现了诊断加权如何根本改变参数后验的取向：稳定几何vs极端稀有事件识别的对比。[page::5-6]

4.2 Lorenz–Rössler：异系统整合验证

• 模型A仍然在Lorenz下表现出稳定几何结构，充当基线锚定。

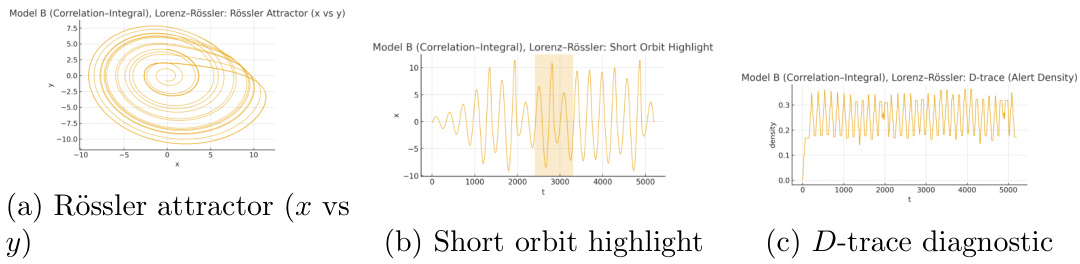
- 模型B在不同的Rössler吸引子上仍能利用Fibonacci诊断捕捉多尺度波动聚集，显示其跨系统的泛化能力。
这表明模型B的统计递归和波动簇集检测框架对动态系统类别具有广泛适用性（见图3、4）。[page::6-7]

4.3 补充基线诊断比较

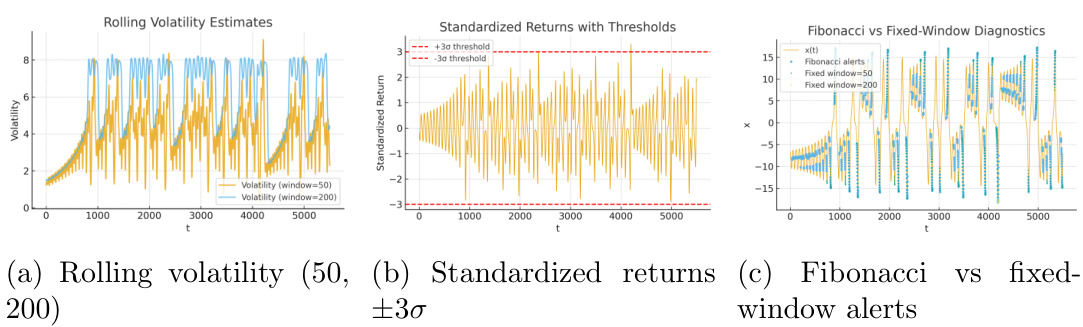
通过固定窗口（50与200）的滚动波动率和标准化收益率进行传统对比。结果表明，传统方法对短时波动突发事件的捕获不足，而Fibonacci窗口诊断能够跨越多个尺度有效识别这些事件（见补充图S1）。这是Fibonacci诊断优于常规方法的实证证明。[page::7-8]

---

5. 讨论

• Model A稳定地将推断锚定于基线几何结构，适合建立系统稳定性的参考框架；

- Model B则突出极端事件的统计聚集特征，通过多尺度Fibonacci窗口实现对极端波动的灵敏捕获，偏重捕捉尾部事件模式，具有创新性。

这种基于诊断权重变化带来的推断差异，为理解复杂系统中常态行为与非常态转变提供了方法论层面的多维视角。[page::8]

---

6. 风险分析的应用意义

两模型为系统性风险评估提供互补视角：

• Model A帮助理解和确认稳定的系统行为模式；

- Model B通过多尺度波动簇集识别低概率高冲击的极端风险事件。

结合这两个视角，可以打造既理解常规风险结构又能预警黑天鹅事件的综合风险管理框架，契合Taleb的理论需求。[page::9]

---

7. 结论

本研究建立了一个双模型框架，将混沌吸引子几何与统计波动簇集整合入贝叶斯推断，既能稳定估计基线几何参数（Model A），又能灵敏提取极端波动簇集特征（Model B）。两模型在同一系统与跨系统测试中表现卓越，展示了模型A提供稳定锚定，模型B提供新颖尾部风险识别的的有力路径。未来工作将扩展至更高维系统及实证数据校准。[page::9-10]

---

8. 未来展望

• 实际金融数据标定；

- 扩展到耦合高维系统，如耦合Lorenz–Rössler；

• 与代理模型集成，连接吸引子动力学与系统性金融网络崩溃机制；

- 优化计算效率以适配大规模ABC-MCMC采样。

目标是实现可应用于预警实际极端风险的实证模型框架。[page::10]

---

三、图表深度解读

图1（页6）—— Model A (Poincaré–Mahalanobis), Lorenz–Lorenz

• 内容： 图1a显示Lorenz吸引子的Poincaré截面点云，重建经典蝴蝶形态；图1b显示基于Poincaré截面计算的参数后验云，明显集中在经典参数$(\sigma=10, \rho=28)$附近；图1c展示MH采样链轨迹，显示参数稳定波动、无明显跳跃。

- 解读： 数据支持基于几何截面进行参数估计的有效性与稳定性，证明模型A能通过几何稳定性准确复现系统动态，为风险基线锚定提供支撑。

• 关联文本： 支持第4.1节论点，模型A成功表现稳定的基础动力结构。

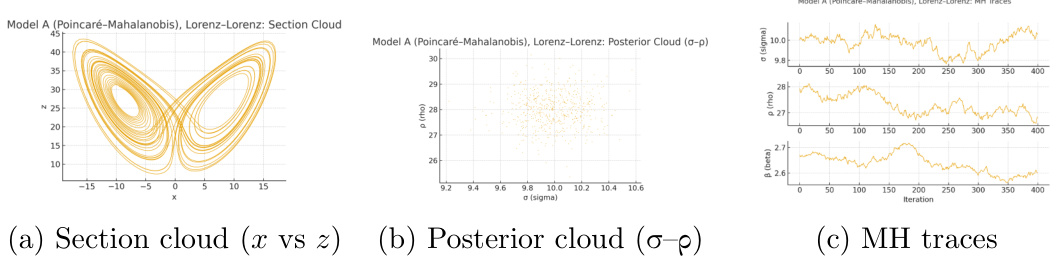
图2（页6）—— Model B (Correlation–Integral), Lorenz–Lorenz

• 内容： 图2a展示波动爆发的短轨道突出区间，图2b呈现$D$-trace诊断曲线，显示波动报警密度随时间的变化及采样接受点（低值处）；图2c为重构吸引子，显示Lorenz动态。

- 解读： 说明模型B敏锐捕获多尺度波动簇集并用Fibonacci窗递归检测极端事件，隐含其对风险极端尾部特征的聚焦效果。

• 关联文本： 与第4.1节模型B侧重尾部风险一致。

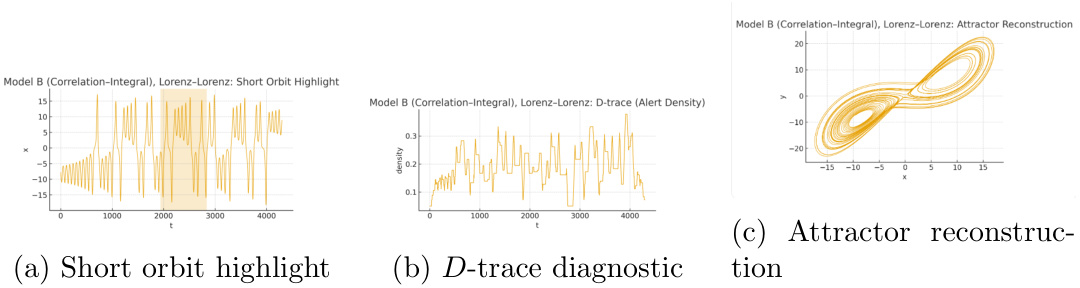
图3（页7）—— Model A, Lorenz–Rössler跨系统锚定

• 内容： 显示作为几何锚的Lorenz吸引子Poincaré截面，维持稳定形态。

- 解读： 作为跨系统模型基准，验证几何稳定性在复杂系统间的通用性。

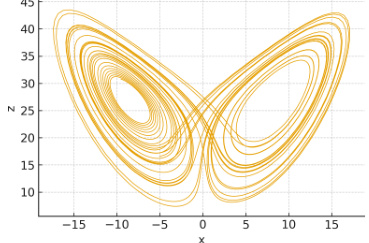
图4（页7）—— Model B, Rössler吸引子与Fibonacci诊断

• 内容： 图4a为Rössler吸引子轨迹呈现典型螺旋结构；图4b突出波动爆发轨迹段；图4c为$\mathcal{D}$-trace，显示诊断距离波动与采样接受时点。

- 解读： 展示模型B成功地将Fibonacci诊断推广至非Lorenz混沌系统，具备跨系统尾部风险捕捉能力。

补充图S1（页8）—— 基线对比诊断

• 内容： S1a为50与200步固定窗口的滚动波动率，S1b展示标准化收益与$\pm 3\sigma$阈值，S1c对比Fibonacci与固定窗口波动报警。

- 解读： 传统固定窗口方法平滑过多，难以捕获短期波动爆发；Fibonacci多尺度诊断敏锐识别多层次极端事件，证实其优越性。


---

四、估值分析

此报告为理论建模和方法论研究，不涉及传统财务估值（如DCF、市盈率等），而是开发风险建模及参数推断方法，故省略常规估值分析。

---

五、风险因素评估

报告关注的“风险”本质是模型中极端事件和波动爆发的正确识别和反映。通过

• Model A确保对系统基线稳定性的稳健估计，从而降低误判风险；

- Model B有效识别极端尾部风险事件，避免忽视黑天鹅风险。

缺乏风险缓解策略的展开，但模型提供的双重识别机制可以作为风险监控的关键组成部分。[page::8,9]

---

六、批判视角与细微差别

• 报告自觉区别两模型定位不同，且实证上模型B牺牲部分轨迹真实性以换取尾部事件捕捉敏感度，暗示模型选择需基于具体风险管理目的；

- 模型在迭代次数（500步）及样本规模上相对较小，未来扩大规模或许更充分揭示后验分布特征；

• 对实际金融市场数据的应用尚未详尽探讨，离理论到实证仍有距离；

- 基于固定时间窗口的传统方法被弱化，需注意在实际应用中两者或可互补；

• 報告默认厚尾先验选择合理性，缺乏详尽先验选择与敏感性分析。

总体而言，报告框架合理，立意创新，但实证验证和应用推广需谨慎。[page::10]

---

七、结论性综合

该报告成功构建了基于贝叶斯推断的混沌吸引子风险模型体系，提出双模型路径：

• Model A扎根于几何分析，确保基础系统结构稳定而准确的估计，为风险分析提供稳定锚定；

- Model B利用相关积分与创新的Fibonacci多尺度波动诊断，精细捕捉极端风险事件的统计聚集特征，从统计视角揭示黑天鹅事件发生机制。

两模型在Lorenz和Rössler系统上的应用验证了理论与方法的有效性和泛化能力。相比传统固定窗口方法，Fibonacci诊断大幅提升了对短时和多尺度波动爆发的监测，进而强化了系统性风险分析工具的能力。

总体而言，报告立场清晰：风险管理应兼顾稳定结构识别与极端尾部事件检测，双模型联合为金融及其他复杂系统黑天鹅风险分析开辟了新路径。此框架未来有望通过实证调校和计算优化广泛应用于金融市场风险管理、气候变化风险预警及其他复杂系统脆弱性分析。[page::0-12]

---

总结

本报告在混沌动力学与贝叶斯推断结合的前沿领域提出了创新方法论，回应了现代风险管理对极端事件建模的迫切需求。通过深入的理论开发、方法设计和数值实验，揭示了两类不同但互补的风险识别机制，促进了对黑天鹅事件成因和检测的新理解，具有重要学术价值和潜在实际应用前景。

报告