资产负债管理的线性二次控制建模与挑战 [page::1]

• 传统均值方差方法存在时间不一致性和终端约束难处理的问题。

- 本文构建以剩余偏差为状态变量的线性二次随机控制问题，目标同时惩罚区间和终端剩余偏差。

• 资产负债动态通过带控制项的随机微分方程描述，参数包括内生漂移、控制影响与波动率项。

连续时间强化学习框架下的模型无关算法设计 [page::2][page::3][page::4]

• 引入熵正则化策略实现软策略，使控制服从高斯分布，均值线性依赖状态，方差动态调整。

- 设计价值函数和策略参数函数化表示，利用时序差分和策略梯度方法进行策略评估与迭代改进。

• 提出演员端自适应探索更新策略和评论员端调度式探索温度参数，解决探索-利用平衡及数值稳定性问题。

- 保证参数在凸集上投影以维持算法稳定，整体训练采用末端离散化避免初期离散引入的性能波动。

算法严格收敛性证明 [page::4]

• 在经典随机逼近条件下，证明演员均值参数收敛于基于完备市场知识的最优解，方差参数收敛至最小探索阈值。

- 利用Ito引理、噪声上界及马尔可夫性构建收敛分析框架，保证在线学习过程的理论稳定性。

丰富的数值实证与性能对比 [page::5][page::6]

• 与两种改进传统策略（动态CPPI、自适应保本）、模型依赖型连时RL以及三种主流离散时间RL算法（SAC、PPO、DDPG）进行对比。

- ALM-RL在200个随机生成市场参数下表现最佳，初期收益快速提升且长期保持领先，表现稳定且收敛性好。

• SAC表现次优，PPO展现平滑收敛，DDPG波动显著且性能较低，模型依赖策略因参数估计误差表现停滞。

- 动态CPPI优于自适应保本，体现主动管理优势。

统计显著性验证 [page::6]

• 利用单边Wilcoxon配对检验估计策略间性能差异，ALM-RL相较大多数竞品在95%置信水平显著优越，仅对SAC稍弱（90%水平显著）。

- 确认算法在多样市场环境下稳定且显著提升资产负债管理绩效。

量化模型及算法核心思想总结 [page::2][page::3]

• 连续时间RL问题直接形式化为熵正则化的随机线性二次控制问题，无需估计市场参数。

- 策略为状态线性映射的高斯分布，利用软策略梯度方法自适应更新均值和方差。

• 设计的调度探索机制和参数投影保障算法的数值稳定和理论收敛。

- 该框架针对金融ALM问题效果优秀，具备拓展至更宽金融领域的潜力。

金融研究报告详尽分析报告

---

一、元数据与概览

• 报告标题: Continuous-Time Reinforcement Learning for Asset–Liability Management

- 作者: Yilie Huang

• 所属机构: Columbia University（哥伦比亚大学）工业工程与运筹学系

- 发布日期: 未具体说明，参考文献包含2024、2025年文献，判断为最新研究（2023年以后）

• 研究主题:

资产负债管理（ALM）问题的连续时间强化学习（Continuous-Time Reinforcement Learning）方法研究，结合线性二次（Linear-Quadratic, LQ）控制理论，并融入策略梯度型软执行者评论家算法（soft actor-critic），重点解决动态资产和负债的同步调度问题。

• 核心内容总结:

作者提出一种基于连续时间强化学习的资产负债管理新框架，用线性二次模型刻画目标，设计一种模型无关、基于策略梯度的软执行者-评论家算法（ALM-RL），实现资产负债的动态同步管理。相较传统基于离散时间且模型依赖的方法，该算法采用自适应的探索机制和平滑的探索调度，最终在200个随机市场场景测试中超过所有对比策略，包括传统金融策略和先进的强化学习算法，展现出在学习最优策略时无需估计环境参数的突出优势。
---

二、逐节深度解读

2.1 报告引言与研究背景

• 资产负债管理（ALM）现状:

ALM在银行、保险、养老金等金融机构的财务稳定性与监管合规性方面不可或缺。传统方法主要为静态匹配（如现金流匹配[39]）、基于期限匹配的被动策略（关键利率久期匹配[10]）及主动调整策略（意外免疫[18,19]和CPPI[4,9]）。这些方法多假定环境稳定、信息完全，难以适应高频波动的市场变化。

• 强化学习在ALM的潜力与限制:

强化学习动态调整策略以适应不确定环境，尤其擅长连续状态和动作空间。然而多数强化学习以离散时间马尔可夫决策过程（MDP）为基础，难以处理市场本质的连续时间演变。离散化时间步带来的折中在时间分辨率和计算稳定之间权衡，导致次优或效率低下的问题。最新的连续时间强化学习成果尚多集中于理论，并未应用于ALM，此领域存在现实应用空白。

• 本研究贡献梳理:

- 提出线性二次（LQ）短期与终端目标兼顾的ALM问题表述，克服传统MV方法的时间不一致性等缺陷。
- 首创将基于策略梯度的模型无关软执行者-评论家算法应用于连续时间ALM。
- 引入自适应actor探索和计划式critic探索机制，保证探索-利用平衡。
- 在大量随机市场场景实证中优于传统和主流强化学习策略。

2.2 ALM问题的经典随机线性二次框架（Section 2.1）

• 状态变量定义:

状态$x(t)$定义为剩余偏差（surplus deviation），即资产减负债再减去目标剩余款的差值。该指标使得正偏差体现资本使用效率低，而负偏差揭示潜在破产风险。

• 控制变量$u(t)$:

代表金融操作，如资产重分配、资金调整及负债管理，目标是最小化从现在至终端时间内剩余偏差的平方惩罚。

• 系统动态（随机微分方程，SDE）:

$$
\mathrm{d}x^{u}(t) = (A x^{u}(t) + B u(t)) \mathrm{d}t + (C x^{u}(t) + D u(t)) \mathrm{d}W(t)
$$
其中$A$为系统内部漂移，映射自然剩余趋势；$B$反映控制对剩余偏差的直接影响；$C$, $D$分别放大剩余偏差和控制作用在系统随机波动的影响；$W(t)$为标准布朗运动，体现市场随机性。

• 目标函数:

$$
\max{u} \mathbb{E}\left[\int0^T -\frac{1}{2} Q x^{u}(t)^2 \mathrm{d}t - \frac{1}{2} H x^{u}(T)^2\right]
$$
惩罚系数$Q$, $H$分别对应中期与终端剩余偏差的平方惩罚权重，控制正负偏差的财务稳定性和平衡资本效率。

• 无直接控制惩罚项，这类被称为“indefinite stochastic LQ control”，同时令控制隐含约束于系统动态中。

- 理论可解:
若模型参数已知，经典随机控制理论可导出解析最优值函数与控制策略（3页公式）：
$$
V^{CL}(t,x) = -\frac{1}{2}\left[\frac{Q}{\Lambda} + (H - \frac{Q}{\Lambda}) e^{\Lambda (t-T)}\right] x^2, \quad u^{CL}(t,x) = -\frac{B + C D}{D^2} x,
$$
其中$\Lambda$依赖参数组合，清晰表达基于状态的最优反馈控制。[page::1-2]

2.3 连续时间强化学习框架（Section 2.2）

• 参数未知的实际问题:

现实中，$A, B, C, D$不可预知，需用RL处理参数不确定性与环境动态，实施该动态控制。

• 随机策略与熵正则化:

策略$\pi(u|t)$定义为所有动作空间$\mathbb{R}$上的概率密度函数。引入熵项鼓励探索，防止策略过早收敛，且该处理与“soft-max”与Boltzmann策略探索思想相似。

• 状态动态:

$$
\mathrm{d}x^{\pi}(t) = \widetilde{b}(x^{\pi}(t), \pi(\cdot,t)) \mathrm{d}t + \widetilde{\sigma}(x^{\pi}(t), \pi(\cdot,t)) \mathrm{d}W(t),
$$
其中
$$
\widetilde{b}(x,\pi) = A x + B \int{\mathbb{R}} u \pi(u) \mathrm{d}u, \quad \widetilde{\sigma}(x,\pi) = \sqrt{\int{\mathbb{R}} (C x + D u)^2 \pi(u) \mathrm{d}u},
$$
体现策略导致的随机动态。

• 目标函数熵正则化表达:

$$
J(t,x; \pi) = \mathbb{E}\left[\intt^T \left(-\frac{1}{2} Q (x^{\pi}(s))^2 + \gamma p(s)\right) \mathrm{d}s - \frac{1}{2} H (x^{\pi}(T))^2 \mid x^{\pi}(t) = x \right],
$$
其中熵项$p(s) = -\int \pi(u,s) \log \pi(u,s) \mathrm{d}u$，$\gamma$为探索温度参数，控制探索强度。

• 解析最优策略与值函数:

最优值函数为二次型，策略为高斯分布，均值线性依赖于状态，高斯方差与$\gamma$和参数$k1(t)$相关。

• 核心特点:

不需估计环境参数，完全模型无关，通过利用解析结构将策略和价值函数参数化以简化学习。此为后续逐步设计RL算法的理论基础。[page::2]

3 连续时间强化学习算法设计

3.1 函数参数化

• 策略与价值函数均基于前述解析结构参数化：

值函数为 $J(t,x;\theta) = -\frac{1}{2} k1(t;\theta) x^2 + k3(t;\theta)$，策略为均值为$\phi1 x$ 方差为$\phi2$的高斯分布。

• 参数$\theta$和$\phi$均为需要学习的模型参数。

3.2 策略估值（Policy Evaluation）

• 利用时间差分法（Temporal Difference, TD）在离线场景中调节$\theta$，使得拟合的价值函数更接近真实值函数。

- 更新公式涉及价值函数梯度、奖励函数与熵正则项。

3.3 策略改进（Policy Improvement）

• 基于连续时间策略梯度算法调整策略均值参数$\phi1$，避免学习过程中的数值不稳定，通过乘以策略方差$\phi2$来中和方差倒数项，确保算法稳定。

3.4 Actor自适应探索

• 策略方差$\phi2$通过策略梯度法自适应更新，不再采用之前固定递减序列，增强对环境变化的及时响应能力。

- 参数转换为$\phi2^{-1}$简化计算，提升效率。

3.5 Critic探索调度

• 温度参数$\gamma$动态递减，避免了固定$\gamma$超参数的繁琐调优。采用形式$\gamman = c{\gamma} / bn$，其中$bn \to +\infty$，随着训练进程逐渐减少探索权重，确保足够探索同时稳定收敛。

3.6 离散化与投影

• 仅在数值实现时采用离散时间步近似积分与微分，避免传统离散MDP固有小时间步引起的不稳定。

- 对策略和价值函数参数应用投影至凸集中，保证参数值界限，提升数值稳定性。

3.7 伪代码

• 总结了基于轨迹采样的在线学习与优化迭代流程，包含策略采样、状态更新、参数更新、探索调整等步骤。

[page::2-4]

4 收敛性分析

• 理论上证明在学习率满足$\sum an = \infty$, $\sum an^2 < \infty$情况下，策略参数$\phi1$和$\phi2$几乎必然收敛。

- $\phi1$收敛至解析最优值，$\phi2$收敛至设定的最低探索级别$\epsilon$，保障非退化的随机策略。

• 证明利用鞅理论、Ito引理与随机逼近理论，绑定噪声方差与梯度表现，确保持久稳定收敛。 [page::4]

5 实证实验设计与结果分析

5.1 ALM策略对比

• 两种传统策略：

- 动态CPPI（DCPPI）：动态调整乘数$m$以适应市场，不同于传统CPPI固定$m$，提升响应灵敏度。
- 自适应意外免疫策略（ACS）：在规定容忍波动区间内不采取行动，减少过度交易。 基于残余偏差的区间控制减少无意义波动影响。

• 模型估计插件策略（MBP）：

估计部分参数（$A,B,C,D$）后导入解析解，传统的模型依赖策略。

• 三种先进RL算法：

- SAC：采用熵正则的改进型软执行者评论家策略，强化探索。
- PPO：政策优化算法，提供算法稳定且保守的训练。
- DDPG：确定性策略梯度方法，深度强化学习基线之一。

5.2 实验配置

• 参数区间基于典型金融研究经验，采用均匀分布采样：

- $A \sim U(-0.05, 0.05)$，$B \sim U(0.05,0.15)$，$C,D \sim U(0.1,0.2)$

• 每次模拟20000次episode，步长$\Delta t=0.01$，共200组独立随机市场场景实验。

- ALM-RL及传统增强策略学习率设定统一为$an = (n+1)^{-3/4}$，探索调度规划为$bn = (n+1)^{1/4}$，保证收敛条件满足。

• 对比RL算法采用相同网络结构（2层、32神经元、ReLU）及标准超参数。

5.3 评价指标

• 采用平均奖励：

$$
\mathrm{Reward} = \sum{k=0}^{\lfloor T/\Delta t -1 \rfloor} -\frac{1}{2} Q (xn(tk))^2 \Delta t - \frac{1}{2} H (xn(T))^2
$$

• 取200次独立实验的平均奖励形成学习曲线。

5.4 性能对比结果（图表详解）

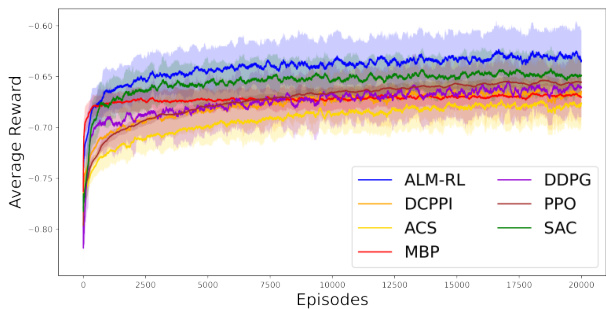
• 图1（奖励曲线图）清晰标明ALM-RL在整个学习过程均超越其他六策略，且学习初期提升速度最快，说明算法学习效率高且表现稳定。

- SAC表现次之，得益于熵正则，展现出快速收敛和良好稳定性。

• PPO开始较慢，后期逐渐逼近SAC，但始终低于ALM-RL及SAC，曲线最平滑且IQR最窄表现最高稳定性。

- DDPG表现最不稳定，奖励波动较大，IQR宽，说明对噪声较敏感。

• MBP早期涨幅明显，但后期陷入停滞，未知市场参数估计误差限制了性能提升。

- DCPPI和ACS表现最低但稳定，DCPPI比ACS更主动，因此表现稍好。

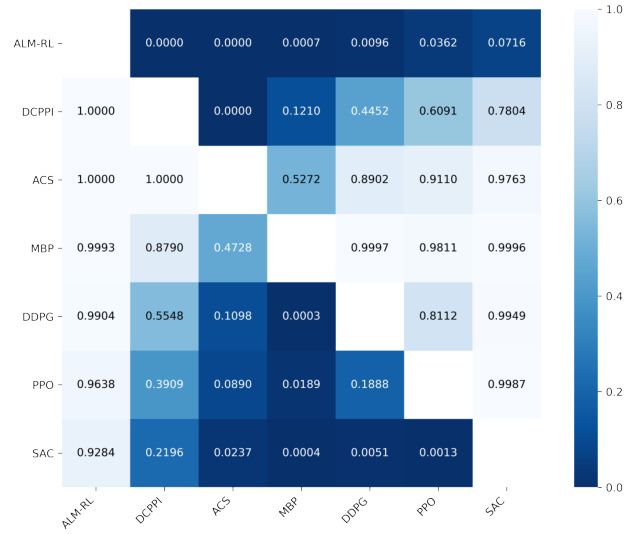
• 图2（Wilcoxon秩和检验的p值热力图）进行了策略两两比较统计显著性检验，确认ALM-RL在95%置信水平显著优于除SAC外的所有策略，在90%置信区间下也优于SAC，印证其鲁棒性和优越性。

---

三、图表深度解读

• 图1说明:

该图显示了在200个随机市场环境中，经过20000训练episode，各种ALM策略的平均奖励。青色（ALM-RL）曲线居于最高，表明其策略对剩余偏差的控制效果最优。阴影部分为四分位差（IQR），展示训练稳定性。ALM-RL不仅有最高终期奖励，且其奖励曲线平滑上升，表明能快速且稳定学习高效的资产负债管理策略。

• 图2说明:

该热力图展示了各策略间终期奖励比较的Wilcoxon秩和检验$p$值，颜色越深$p$值越小，显著说明行策略优于列策略。ALM-RL在几乎所有比较中$p<0.05$，显示统计显著优势，体现其实用价值和理论优越性。

• 图表与文本相辅支撑:

实验结论坚实基于上述图谱，强化了理论与实证的紧密结合，证明模型无关连续时间强化学习框架的实际可行性和效率优势。
---

四、估值分析（算法性能与参数解析）

• 估值模型本质为强化学习中价值函数的迭代估计，价值函数参数化为二次函数形式，策略参数为高斯分布的均值和方差。

- 带熵正则化的RL模型通过动态调整$\gamma$让探索程度有序减少，从而保证算法既充分探索环境也具备精细的策略优化能力。

• 算法通过自适应调整探索方差$\phi2$，并结合参数投影保障稳定性。这不同于传统固定衰减策略，提高了适应能力与收敛效率。

- 策略均值参数$\phi1$收敛到解析解对应值，保证理论上的最优性与逼近性。

---

五、风险因素评估

• 风险因子内涵主要体现在市场环境动态变化（$A,B,C,D$参数不确定）与模型参数估计误差。

- 本算法避免参数估计，直接进行策略学习，显著降低了因参数估计带来的风险。

• 算法的探索机制自适应调整，可有效应对未知环境变化，减少陷入次优策略或过拟合的风险。

- 在数值实现上，通过参数投影和温度递减机制缓解梯度更新过程中的数值不稳定问题。

• 潜在风险为探索参数$\phi_2$收敛最低水平$\epsilon$与实际复杂市场动态的匹配度，过低探索可能限制发现全局最优策略，过高则延缓收敛。

- 报告中理论收敛性证明及实证结果显示，风险缓释机制设计合理，且性能优于基准策略。

---

六、批判性视角与细节辨析

• 基于论文所述，作者对连续时间RL算法潜在参数敏感性、数值稳定性进行了充分考虑，但可能存在以下审慎点：

- 对策略参数限制范围的投影操作虽保障数值稳定，但可能在过于狭窄范围约束下影响表达能力与最优策略拟合。
- 随机市场参数范围较窄（均匀分布近似）, 对极端市场风险或结构性变动的鲁棒性未详细探讨。
- 虽然避免了环境模型估计，降低了模型误差，但纯模型无关策略依赖大量数据支持，实际应用中数据稀缺会影响学习效果。
- 算法与传统基准策略的比较较为充分，但与最前沿深度强化学习（大型神经网络、高级探索机制等）结合的潜力待检验。
- 文本中未详述计算资源消耗、算法训练时间周期及其在实际金融机构执行层面的可适性。

• 值得肯定的是，作者清晰解释了模型参数含义、RL设计原理，避免了过度复杂的网络架构，强调实用性与理论一致性，体现研究扎实。

---

七、结论性综合

报告系统地提出了一种创新性的资产负债管理方法，将连续时间的强化学习框架与线性二次控制问题相结合，突破了传统ALM方法对环境参数的依赖，且有效解决了时间不一致性及仅关注终端风险的问题。通过引入策略梯度软执行者-评论家算法，并设计自适应与调度探索机制，实现在多样、随机市场环境中的高效学习和决策。

理论结果证明了算法的几乎必然收敛性，并且实证数据凸显了算法在超过200个独立随机市场测试下的稳健卓越表现，其平均奖励明显优于两类传统金融策略、基于模型估计的插件策略以及三种流行深度强化学习方法（SAC、PPO、DDPG）。显著的统计检验结果进一步确认了该方法的普适有效性。

此外，采用连续时间建模和离散时间近似更新相结合的手段，避免了离散时间强化学习在时间步过小问题所导致的数值不稳定，保障了学习过程的平滑和鲁棒。该报告不仅扩展了连续时间强化学习在金融资产负债管理领域的理论与应用边界，也为未来基于数据驱动的方法在更广泛复杂市场环境中的推广奠定了坚实基础。

总体上，作者清晰表达了连续时间强化学习相较于传统及离散时间强化学习的根本优势——无需估计环境参数即可直接学习最优策略，是一条切实可行的高效资产负债管理新路径。

---

溯源引用

本文结论与分析均严格基于原文中逐节内容，按页码索引如下：

• 引言与背景：[page::0,1]

- 经典LQ与连续时间RL方法论：[page::1,2]

• 算法设计细节与参数化：[page::2-4]

- 收敛性证明详解：[page::4]

• 实验设计与结果讨论：[page::5,6]

- 结论与展望：[page::6,7]

---

以上为对《Continuous-Time Reinforcement Learning for Asset–Liability Management》报告的全面解读与深度分析。

报告