SOFR利率表现的跳跃结构及建模动机 [page::1]

• 受中央银行政策会议驱动，隔夜利率在确定性日期呈现跳跃现象，经典短期利率模型难以捕捉该特征。

- 引入随机不连续性的扩展CIR模型以兼顾跳跃和非负性，符合当前利率环境的需求。

扩展CIR过程定义与存在唯一性定理 [page::2][page::3]

• 扩展CIR过程为带有纯跳跃部分的非负强解随机微分方程，跳跃发生在确定时间点，跳跃大小依赖跳跃前状态。

- 跳跃分布通过运输映射函数$F_n$与独立均匀随机变量构造，实现状态相关的跳跃机制。

• 证明跳跃时点不可在有限时间内累积且跳跃大小满足可接受性条件，实现整个过程的非负性和存在唯一性。

跳跃之间的状态相关性与跳跃测度对补偿器性质 [page::4]

• 跳跃大小函数依赖于跳跃前状态，导致跳跃序列存在自相关性，区别于传统独立跳跃模型。

- 随机测度补偿子是确定性的，跳跃机制对应的随机测度补偿算子明确，适合在仿射半鞅框架下处理。

扩展CIR过程的仿射性质及充分条件 [page::5][page::6][page::7][page::8]

• 仿射过程定义及扩展到存在确定性跳跃的半鞅设定。

- 充分条件：跳跃条件特征函数满足特定的指数仿射形式，并满足解析延拓及渐近约束。

• 证明若满足条件，存在唯一仿射半鞅解，过程保持非负且满足准正则性(quasiregularity)。

- 跳跃时递归性质及Riccati方程递推公式给出，确保仿射结构。

两个典型仿射跳跃模型示例及数值模拟 [page::9][page::10][page::13]

• 例1：“跳跃至0后再上升”，跳跃后状态为零加一非负仿射随机变量（Gamma分布），既允许向上又允许向下跳跃且保持非负。

- 例2：通过确定性时间变换改造标准CIR，产生跳跃，跳跃大小分布为带位移非中心卡方分布，跳跃之间存在状态相关性。

• 模型适用于有确定性跳跃时点的短期利率及波动率建模，跳跃大小协方差可显式计算。

仿射过程的必要条件及支撑性质 [page::14][page::15]

• 完整支撑(convex span)条件刻画，要求跳跃后状态的支撑覆盖整个非负半轴。

- 若跳跃大小不满支撑条件，如固定正跳，则无法保证仿射过程的完整支撑，影响过程结构。

• 定理给出仿射半鞅存在的充分且必要条件，统一了跳跃函数的形式与支撑范围。

无限可分性的刻画与充分条件 [page::16][page::17][page::18]

• 跳跃的条件特征函数若满足Lévy–Khintchine表示，则达到无限可分条件。

- 需满足扩散部分消失，漂移和Lévy测度有明确非负半轴支持和积分条件，确保非负性和模型可行性。

• 证明了含跳跃的扩展CIR过程在该条件下存在唯一无限可分仿射半鞅解。

- 经典例子（时间变换CIR模型）属于此类，过程保留无限可分性。

关键图示总结

• SOFR利率跳跃图（图1）体现建模背景。

- 仿射跳跃CIR数值模拟（图2，图3）直观展示模型跳跃行为及状态依赖特征。

报告详细分析报告——《AN EXTENDED CIR PROCESS WITH STOCHASTIC DISCONTINUITIES》

---

1. 元数据与报告概览

• 报告标题： AN EXTENDED CIR PROCESS WITH STOCHASTIC DISCONTINUITIES

- 作者： Claudio Fontana, Simone Pavarana, Thorsten Schmidt

• 发布日期： 报告为预览版，时间背景示意为2025年及之前的文献引用和数据。

- 发布机构： 无直接给出，作者分别来自意大利帕多瓦大学数学系和德国弗莱堡大学随机数学系。

• 主题： 本文聚焦于金融数学中的短期利率建模，特别是对经典Cox–Ingersoll–Ross (CIR)过程的扩展，加入了预定且状态依赖的跳跃（stochastic discontinuities），旨在更准确模拟利率市场中（如SOFR）表现出的跳跃特性。

- 核心论点：
- 提出一种结合预定确定时间跳跃的扩展CIR模型，跳跃大小由跳跃前状态决定，允许正向与负向跳跃，进而能捕捉实际市场中货币政策会议等引起的利率突然变动。
- 建立该模型的存在唯一性条件，给出其保持亲和性（affine property）的充分必要条件。
- 通过时间变换构造方法生成该模型，且确保过程的非负性与亲和结构。
- 进一步，分析该扩展过程的无限可分性条件，为相关金融衍生品定价与风险管理奠定理论基础。

• 贡献亮点：

- 将确定性跳跃嵌入经典CIR模型，并保持其数学结构完整。
- 跳跃分布可依赖前跳状态，带来跳跃的自相关性，更符合市场实测数据。
- 完整的数学证明架构涵盖存在唯一性、条件推导及范例展示。
- 将拓展思路应用于利率和波动率建模，具有广泛应用潜力。[page::0,1,2]

---

2. 逐节深度解读

2.1 引言（Section 1）

• 关键论点及背景：

- 近期利率市场尤其以SOFR为例，表现出在央行会议等预定时间出现跳跃特征（Figure 1）。
- 经典短期利率模型（如CIR模型）无法捕捉此类跳跃，尤其是跳跃大小和方向依赖当前状态的特征。
- 既有文献（Fontana et al. 2024等）主要扩展Hull–White模型，使用独立、正向高斯跳跃，本报告扩展到非负的CIR过程并允许状态相关的跳跃，呈现更真实的风险结构和市场震荡。

• 数学及金融动机： COVID-19疫情后，货币政策紧缩导致利率结构急剧变化，禁止负利率趋势使得CIR成为更合适的建模工具。

- 结构说明：
- Section 2介绍带跳跃的CIR定义及存在唯一性。
- Section 3探讨亲和性质并提供建构例子与仿真。
- Section 4分析无限可分性条件。[page::0]

2.2 扩展CIR过程定义及存在唯一性（Section 2）

• 定义及模型描述：

- 扩展CIR过程$Xt$满足如下SDE：
$$dXt = \kappa(\theta - Xt) dt + \sigma \sqrt{Xt} dWt + dJt,$$
其中跳跃组件：
$$Jt = \sum{n:sn \le t} Fn(X{sn-}, Zn),$$
跳跃时刻$sn$为确定性递增序列，跳跃函数依赖于跳前状态$X{sn-}$及均匀随机变量$Zn$。

• 重要条件及概念：

- 跳跃非积累假设（Assumption 2.3）： 跳跃时刻序列无有限时间内累积点，保证模型数学可行性。
- 跳跃可接受性（Definition 2.5）： 保证跳跃后结果非负，数学条件为跳跃幅度几乎处处不小于$-x$，避免过程越界。

• 存在唯一性定理（Theorem 2.7）： 在上述假设和条件下，存在唯一非负强解。证明通过区间递归拼接标准CIR解和跳跃调整。

- 跳跃的马氏性质： 利用随机测度$\mu$和其补偿测度$\nu$，将跳跃部分表达为鞅，$\nu$为确定性测度，与Poisson过程不同但规律可控。

• 跳跃自相关特性（Proposition 2.11）：

跳跃大小之间存在非零协方差，协方差由跳跃函数条件均值决定，体现前序状态依赖引发的自相关。此特性显著区别传统独立跳跃模型。

• 与已知Hull–White扩展模型区别： 后者跳跃独立、正向，本模型允许正负跳跃且跳跃间相关。[page::1,2,3,4,5]

2.3 亲和性质的理论框架与条件（Section 3）

• 亲和过程定义：

过程$X$在状态空间$D \subset \mathbb{R}^d$是亲和的，指其特征函数条件期望呈指数仿射形式
$$E[e^{\langle u, XT \rangle} | \mathcal{F}t] = \exp(\phit(T,u) + \langle \psit(T,u), Xt \rangle),$$
其中$\phit, \psit$为连续函数满足一定正则性。

• 跳跃亲和条件：

- 跳跃大小$Fn$的条件特征函数需呈仿射形式：
$$E[e^{u Fn(X{sn-}, Zn)} | \mathcal{F}{sn-}] = \exp(\gamma{n,0}(u) + \gamma{n,1}(u) X{sn-}), \quad u \in i\mathbb{R},$$
并满足解析延拓及边界行为（Lemma 3.1）。
- 这些条件确保跳跃本身的分布支持非负，满足模型的非负限制。

• 充分条件定理（Theorem 3.3）： 在满足上述仿射条件及无跳跃聚积前提下，扩展CIR过程为准正规亲和半鞅，唯一存在。

- 证明策略：
- 利用连续CIR过程的亲和性质分段递归构造跳跃间的特征指数函数$\phi, \psi$。
- 验证归一性和连续性。

• 亲和过程具体构造范例（Section 3.2）：

1. 跳跃先降为零后加正态随机变量（Example 3.5），跳跃大小形式如$Fn(x,z) = -x + fn(x,z), fn \ge 0$，其中$fn$符合Gamma分布的随机变换，保证非负，允许上下跳跃。
2. 通过确定性时间变换构造（Proposition 3.7）：将经典CIR用带跳跃的时间变换$\tau(t)=t+H(t)$生成跳跃，跳跃量为CIR过程在时间段的增量，带有非中心卡方分布，保持亲和性。

• 示例图表：

- Figure 2模拟上述第一个示例，展示具有跳跃的CIR轨迹，跳跃点标明前后状态。
- Figure 3模拟第二个时间变换示例，跳跃距离对应非中心卡方分布。

• 跳跃的充分必要条件完整刻画（Theorem 3.12）：

连续$Fn$且满足支持空间充满条件，跳跃大小条件特征函数必须为仿射形式，状态加跳跃保持全空间$\mathbb{R}+$。

• 支持空间完整性说明（Lemma 3.9）：

确保跳跃后过程支持为$\mathbb{R}+$，需跳跃对应函数在$(x,z)$域上下界分别为0和无穷大。

• 违反条件示例（Example 3.11）： 固定单位正向跳跃导致跳跃支持下界不为零，违背全空间支持条件。

- 注释： 亲和模型的递归半流性质和数学正则性条件保证实用性与分析便利。[page::5,6,7,8,9,10,11,12,13,14,15]

2.4 无限可分性条件（Section 4）

• 定义及动机：

无限可分性指过程在任何时间段的转移分布都可看作某个分布的多次卷积，自然对应带有Levy-Khintchine形式的特征函数。
- 连续CIR过程本身为无限可分过程。
- 期望扩展过程跳跃分布同样具有该性质，实现过程整体无限可分。

• Levy-Khintchine表示法条件（Lemma 4.1）：

- $\gamma{n,0}$和$\gamma{n,1}$需具备Levy-Khintchine形式。
- 扩散项需消失（无二阶项），跳跃测度$\nu{n,j}$支持于非负轴。
- 漂移系数满足$\beta{n,0}\ge 0, \beta{n,1} \ge -1$。

• 充分条件及存在唯一性（Theorem 4.3）：

满足跳跃分布Levy-Khintchine条件后，扩展CIR过程存在唯一无限可分准正规亲和半鞅解。

• 证明要点：

- 利用上一节仿射性及跳跃分布特征函数结构。
- 创造改进参量集满足文献中可接受条件。
- 调用Keller-Ressel等（2019）中定理保证解存在。

• 补充说明（Remark 4.4）：

- 充分必要条件几乎一致，示例中介绍的两种跳跃模型均属于无限可分过程。
- 时间变换保留无限可分性属性，符合经典随机过程定理。

• 总结： 该部分完成了扩展CIR过程理论体系的完善，为进一步期权定价、风险管理等应用提供基础。 [page::16,17,18]

---

3. 图表深度解读

图表1 (Page 1)

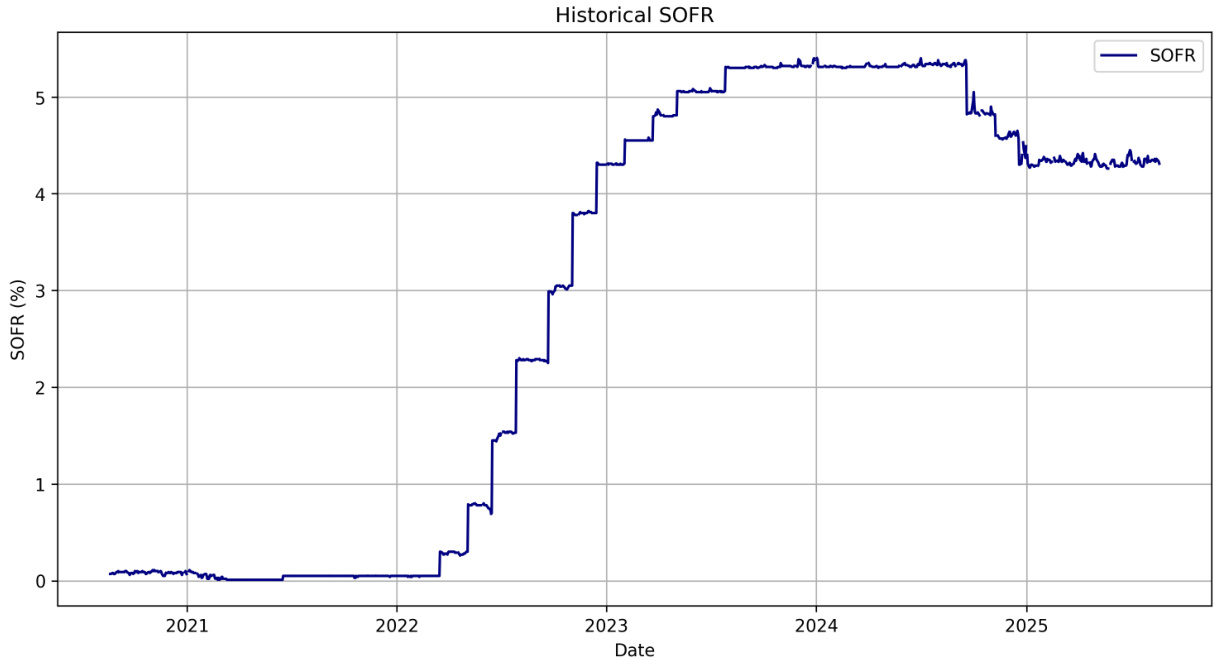
• 内容描述： SOFR（美国担保隔夜融资利率）历史数据，显示2020-2025年间利率多次跳跃，跳跃时间多为央行会议等预定事件。

- 解读：
- 连续期间价格平稳，有明显阶梯式跳升及跳降。
- 数据强烈支持考虑跳跃因素的短率模型。

• 联系文本： 展示模型研究背景及实际动机，凸显仅用连续扩散模型难以拟合实际利率的跳跃行为。[page::1]

图表2 (Page 10)

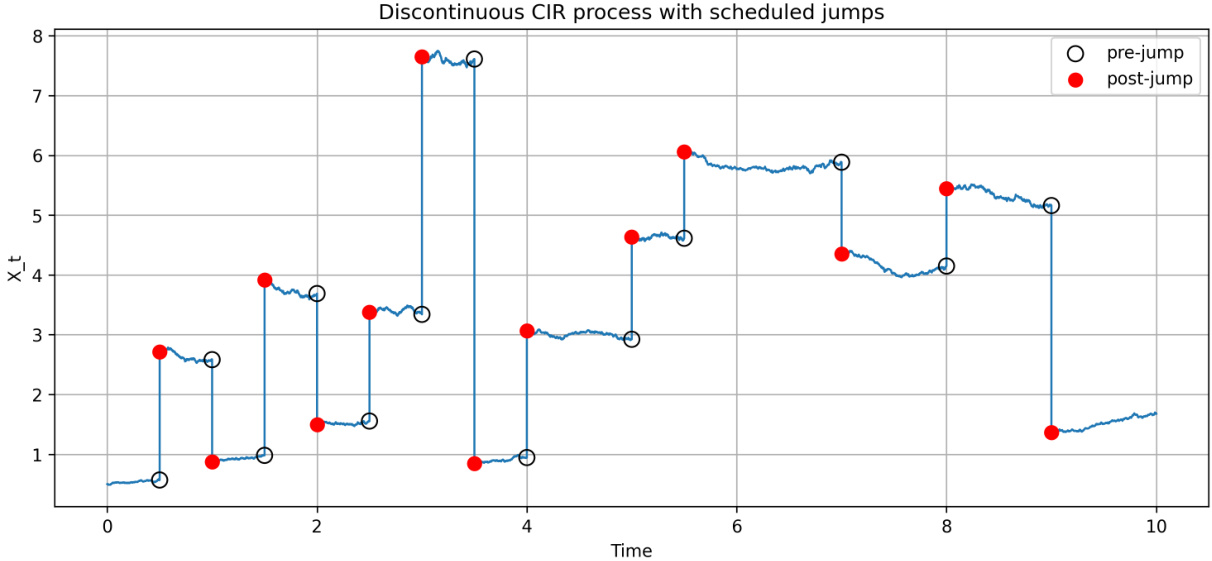
• 内容描述： 模拟基于Example 3.5构造的扩展CIR过程，设定参数$\kappa=0.1$，$\theta=3.0$，$\sigma=0.1$，13次预定跳跃，跳跃后状态服从状态依赖Gamma分布。

- 解读：
- 蓝色曲线为过程轨迹，黑色圆点表示各跳跃前的状态，红色圆点表示跳跃后的状态。
- 跳跃显示正负两种方向，非对称震荡特征明显。
- 跳跃幅度和频率符合市场观察特点，模型成功捕捉跳跃依赖状态的性质。

• 联系文本： 直观展示了带跳跃扩展CIR特点与模型可模拟复杂跳跃行为的能力。[page::10]

图表3 (Page 13)

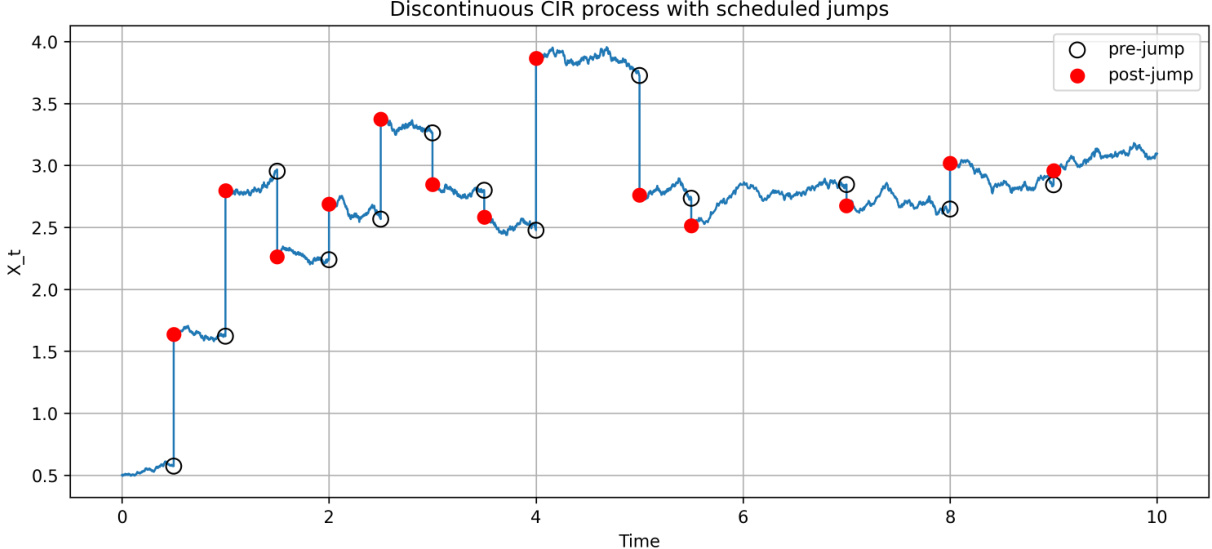
• 内容描述： 基于确定性时间变换的扩展CIR过程模拟，参数同上，13个跳跃，跳跃幅度服从非中心卡方分布。

- 解读：
- 跳跃幅度较前图小，过程更偏向连续，但同样存在离散跳跃。
- 跳跃间存在自相关，体现时间变换引入的统计依赖性。
- 模拟结果反映了时间变换方法的有效性和灵活性。

• 联系文本： 证明基于时间变换方法建模的扩展CIR过程仍保持亲和性和非负性，且更贴合金融市场跳跃特性。[page::13]

---

4. 估值分析

报告主体为数学模型构建与性质分析，未直接涉及具体资产定价，但理论基础对估值模型至关重要。

• 估值隐含工具：

- 亲和模型的特征函数指数仿射形式便于半解析计算债券、利率衍生品定价。
- 时间变换及跳跃结构可嵌入风险管理和期权估值模型中。
- 无套利环境通过保留亲和结构和有限变差条件得到保证。

• 关键输入假设：

- 跳跃时刻确定且不聚集。
- 跳跃大小与过程状态关联，满足非负限制和条件特征函数结构。

• 推断： 本文构建的扩展CIR模型若用于估值，将通过其条件特征函数递归公式，高效计算期望值和定价偏导数，弥补传统CIR模型的跳跃缺陷。

---

5. 风险因素评估

• 主要风险因子：

- 跳跃时刻聚积风险：无限多个跳跃聚集于有限时间内将破坏模型存在性。
- 跳跃幅度不当风险：若跳跃大小不满足“跳后非负”条件可能导致状态空间越界。
- 模型假设风险：跳跃大小函数依赖性假设及正态或Gamma分布形式可能不完全拟合实际。
- 度量变换稳定性风险：时间变换假设的理想性在实际估值中可能带来偏差。

• 潜在缓解策略：

- 设定合理跳跃序列及分布参数。
- 确保严格满足数学假设条件，提升模拟和估计的稳定性。
- 有限跳跃处理技巧及跳跃幅度动态调节。

• 模型优势减少部分传统风险点，特别是其通过跳跃前状态依赖加强了风险表征。

---

6. 审慎视角与细微差别

• 模型的限制与潜在弱点：

- 跳跃大小函数$Fn$需满足严格的连续性与解析延拓等数学条件，实际建模时参数识别难度较大。
- 时间变换构建虽然理论严谨，但在极端市场情况（如巨大跳跃，复杂利率政策变化）下的适用性和鲁棒性尚待检验。
- 无跳跃间相互作用假设较强，模型未考虑跳跃间可能存在的非线性联动。

• 假设的稳健性：

- 跳跃时刻确定且非积累的设定可能忽视某些不确定跳跃时点，限制模型对更广泛市场事件的适应力。

• 内部一致性良好，跳跃的状态依赖引入的自相关统计特性合理且创新，但对模型复杂度及计算效率的影响未具体展开。

---

7. 结论性综合

本文系统构建并深入分析了带有随机跳跃但跳跃时点确定且跳跃大小状态相关的CIR过程的扩展模型，且证明：

• 在跳跃时间不聚积、跳跃大小满足非负条件下，模型存在唯一且路径非负的强解。

- 模型自然继承CIR的亲和性，条件特征函数具有指数仿射形式，保证经典金融工具估值的数值可行性和理论严谨性。

• 跳跃大小的状态依赖引入了跳跃间的自相关性，真实体现金融市场中利率跳跃的时间结构和统计特性。

- 利用确定性时间变换方法方便地构造了此类模型，且跳跃变换具有非中心卡方分布性质，数理统计可明确量化。

• 通过Levy-Khintchine公式，完整刻画了无限可分性的充分必要条件，为更复杂市场风险和衍生品定价奠定基础。

- 模型仿真图（Figures 1-3）直观验证理论分析，支持该扩展CIR过程能较好复刻市场跳跃现象。

总体来看，报告提出了一套高度数学化且具有现实金融适用性的新型短期利率建模范式，填补了传统CIR模型对预定跳跃特征捕捉的不足。其结构严谨、理论基础坚实，为后续开展金融产品设计、风险管理提供重要工具与思路。

---

全文引用页码： [page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]

附图索引

• — Figure 1：SOFR历史跳跃

- — Figure 2：仿真示例1（跳跃先降至零）
- — Figure 3：仿真示例2（时间变换法）

报告