研究背景与目的 [page::0][page::1]

• 现有研究证实金融波动率具有长记忆特征，传统模型基于Hurst参数H>0.5的长记忆随机波动率。

- 新兴粗波动率模型采用H<0.5以揭示高频路径不规则性，估计H是区分模型的关键。

• 本文创新性采用Kolmogorov-Smirnov统计量比较整个分布而非单点矩估计Hurst指数，解决传统方法非线性偏差问题。

估计方法与理论创新 [page::2][page::3][page::4][page::5][page::6][page::7][page::8]

• 定义H-自相似过程及其增量分布，利用Kolmogorov-Smirnov (KS) 统计量度量不同时间尺度归一化增量分布差异，以定位H的最优估计值。

- 提出随机置换方法，通过打乱序列顺序以去除自相关，保持边际分布不变，实现KS统计量在依赖数据上的有效性（满足近似白噪声性质）。

• 推导出估计量的渐近方差表达式$Var(\hat{H}0) \approx \frac{2\pi e}{(\ln a)^2}\left(\frac{1}{\sqrt{n}}+\frac{1}{\sqrt{m}}\right)^2$，支持置信区间构建与统计推断。

理论解释波动率粗糙度差异 [page::9][page::10][page::11][page::12][page::13]

• 通过波动率的积分和平滑运算，理论上VIX（隐含波动率）由于包含条件期望及未来积分，正则性增强，Hurst指数高于实现波动率。

- 证明方差不等式显示实现波动率方差大于VIX，粗糙度（Hurst指数）满足$H{VIX}>H_{RV}$。

• 引用多分纲随机指数过程说明方差与规则性呈负相关，进一步佐证实证观察。

估计算法与效率比较 [page::13][page::14][page::15]

• 网格搜索（GS）虽简单稳健，但计算量随步长减小呈线性增长，不适合大规模应用。

- 提出并比较多种无导数优化算法，包括遗传算法、模拟退火、粒子群、直接搜索、Brent法、Nelder-Mead法。

• 结果表明Brent法和Nelder-Mead法在计算效率上优于其他算法，且估计精度相近，极大提升估计的实时可行性。

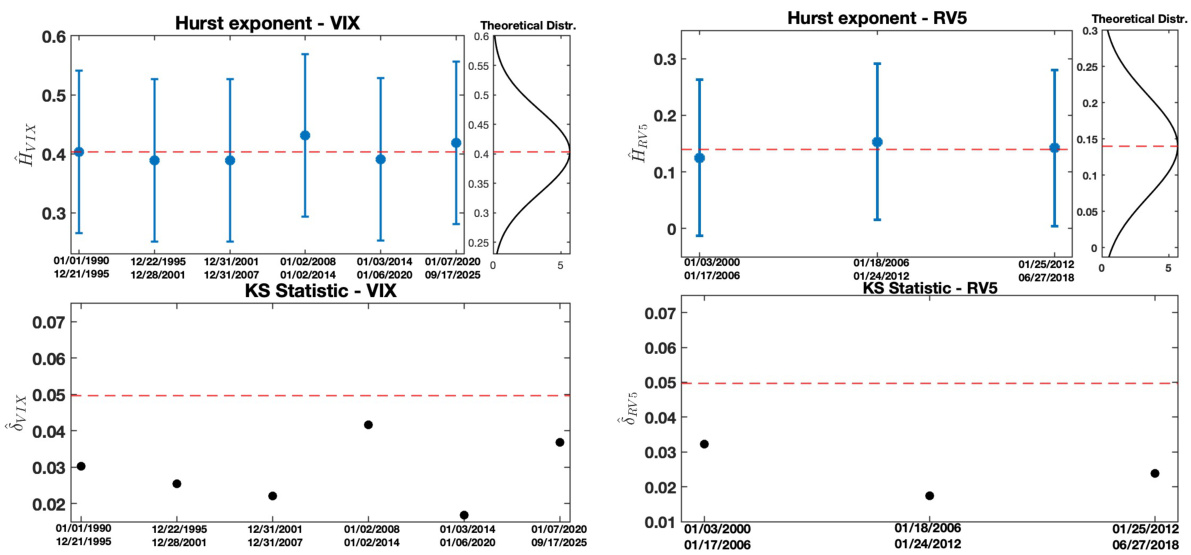
实证分析结果 [page::16][page::17]

• 对1990-2025年CBOE VIX对数与2000-2018年标普500指数5分钟实现波动率对数系列应用估计方法。

- VIX的Hurst估计约为0.40，5分钟实现波动率约为0.14，两者均远低于0.5，且VIX稳态更加平滑。

• KS统计量均小于5%临界值，验证估计方法有效性。

- 统计检验显著支持假设：VIX比实现波动率规则性更强，符合理论假设和先前研究结论。

结论与贡献 [page::18]

• 本文创新地基于分布的KS统计量结合随机置换处理，解决了时间相关金融数据中Hurst估计的关键难题。

- 推导出估计量的渐近性质并通过高效优化算法确保计算可行性。

• 理论与实证证明隐含波动率比实现波动率更平滑，强化粗波动率建模框架。

- 结果揭示Hurst参数同时反映局部粗糙度与长记忆，提示未来需发展分离模型解决此长期难题。

金融研究报告深度解析报告

论文题目

Roughness Analysis of Realized Volatility and VIX through Randomized Kolmogorov-Smirnov Distribution

作者与机构

Sergio Bianchi, Daniele Angelini
MEMOTEF, Sapienza University of Rome, Italy

发布时间与核心主题

发布时间未明确指示，结合文中资助年份推测约为2024年初。主题聚焦于金融市场波动率的粗糙度分析，特别着眼于隐含波动率（VIX指数）和实际波动率两者的比较，采用一种基于Kolmogorov–Smirnov统计量的新的赫斯特指数估计方法，旨在刻画波动率动态的粗糙性质及其统计显著性。

---

一、报告概览与核心论点

报告提出了一个创新的基于分布的赫斯特指数估计器，利用Kolmogorov–Smirnov（KS）检验进行全分布的尺度行为测度，而非传统的基于矩的方法，从而能够更丰富捕捉分布结构信息并降低偏差。为应对金融波动率时间序列的强依赖性，报告引入随机置换方法去除序列自相关且保持边缘分布，确保KS检验适用性和统计推断的严谨。最终，应用于VIX指数与S&P500的5分钟高频实现波动率揭示了两者粗糙度存在显著等级：隐含波动率更为平滑，但两者均体现远低于0.5的赫斯特指数，印证粗糙波动率理论。同时指出分离局部粗糙性和长记忆效应的建模挑战尚未解决。

---

二、逐章节深度解读

1. 引言

文献回顾指出资产价格波动性的持久性，导致采用长记忆模型如Fractional Stochastic Volatility (FSV, $H>1/2$)模型。随后近年研究转向粗糙波动率模型（Rough Fractional Stochastic Volatility, RFSV），其特征为$H<1/2$，呈现高度不规则的路径。强调了粗糙度与长记忆效应在分数布朗运动中不可分离的本质难题。文中提及尝试同时整合粗糙性和慢衰减自相关的新兴模型[9]，突显了识别赫斯特指数的重要性。

2. 方法论

2.1 赫斯特指数与自相似性定义

• 自相似过程定义：满足尺度缩放分布不变性，表达式为\[(X{a t1}, ..., X{a tk}) \stackrel{d}{=} (a^{H} X{t1}, ..., a^{H} X{tk})\]。

- 增量过程自相似性：若$Xt$为自相似进程且增量平稳，则增量过程同样具备相同的自相似指数$H$。

• 统计限制：单路径观测限制只能估计边缘分布，无法估计多维联合分布，因此报告提出的方法检测的是必要条件，不足以确认自相似性。

2.2 基于Kolmogorov-Smirnov统计的估计方法

• 通过比较不同尺度下的分布来寻找最小KS统计量对应的$H0$。

- 呈现理论基础与性质（Propositions 2.1 ~ 2.3），包括KS距离关于$H$的单调特性和唯一极小值存在性，保证该最小值对应真正的赫斯特指数。

• 估计具体表达式为：\[\hat{H}0 = \arg\min{H\in(0,1]} \hat{\delta}{Zt}(\PsiH)\]，通过求取缩放后增量分布的最大距离最小化实现。

2.3 解决时间序列自相关依赖的随机置换技术

• 利用随机区块置换构造序列，使得自相关结构在大块置换后被破坏（趋向白噪声），同时边缘分布保持不变（Proposition 2.4）。

- 随机置换保证KS统计量满足独立样本条件，允许显著性测试。

• 理论证明了随机置换破坏多维自相似结构（$k\geq 2$）的概率极为高，故该方法仅检验分布尺度一致性（边缘级别 $k=1$），属必要条件（Proposition 2.5）。

2.4 估计器方差估计与统计推断（Proposition 2.6）

• 在增量服从正态分布且由随机置换消除自相关后，推导出估计器方差近似公式为

\[
\operatorname{Var}(\hat{H}0) \approx \frac{2 \pi e}{(\ln a)^2} \left( \frac{1}{\sqrt{n}} + \frac{1}{\sqrt{m}} \right)^2,
\]
其中$n,m$为两个样本大小，$a$为尺度因子。

• 利用高斯CDF差的灵敏度与Dvoretzky-Kiefer-Wolfowitz不等式，结合估计器的渐进性质，得出收敛速度和标准误估计。

- 为统计检验和置信区间提供理论支持。

3. VIX与实现波动率的粗糙度比较（理论与实证）

3.1 理论基础

• 说明实现波动率作为过去波动的积分（积分算子平滑），会比即刻波动率更光滑，即

\[
H{\text{realized}} > H{\text{spot}}.
\]

• VIX为基于风险中性概率的未来方差预期，结合积分和平滑的条件期望运算，因而其正则性更强，即

\[
H{\text{VIX}} > H{\text{realized}} > H{\text{spot}}.
\]

• 提出Proposition 3.1证明了条件方差小于原始随机变量的方差，及其平方根变换后的方差不等式，严格支持该不等式关系。

3.2 经验意义

• 该比较理论解释为何市场隐含波动率平滑度高于历史实现波动率，符合文献如[28,27]发现。

- 讨论多重分数指数随机过程（MPRE）框架下，方差与赫斯特指数的反比关系支持粗糙度与方差规律。

4. 优化方法与计算效率

• 初始用网格搜索（Grid Search, GS）方法寻找使KS统计量最小的$H$，但计算成本高，尤其网格细化时。

- 对比包括遗传算法(GA)、模拟退火(SA)、粒子群(PS)、直接搜索(DS)、Brent及Nelder-Mead等无导数优化算法的性能。

• 图1显示GS耗时高出1-2个数量级，无导数方法尤其Brent与Nelder-Mead收敛速度快，准确度相当，推荐用于大规模估计。

5. 数据与应用

5.1 数据来源

• VIX对数，1990年1月2日至2025年9月17日，共9018个观测点。

- S&P 500 5分钟实现波动率对数，2000年1月3日至2018年6月27日，共4713个观测点。

5.2 估计实施参数

• 选用尺度区间$\underline{a}=1$，$\overline{a}=21$，子序列长度$T=\nu-\overline{a}$，置信区间宽度$\pm 0.1378$。

- 应用Brent优化方法估计静态赫斯特指数。

5.3 实证结果（图2详解）

• VIX赫斯特指数$\hat{H}{\text{VIX}}$约为0.40，稳定跨越不同时期，95%置信区间覆盖均值，且KS统计量均显著低于临界值。

- 实现波动率赫斯特指数$\hat{H}{\text{RV5}}$约为0.14，同样表现稳定且KS检验通过。

• 统计检验结果极显著证实$H{\text{VIX}} > H{\text{RV5}}$，表明隐含波动率更平滑（z=2.6636, p=0.0037）。

- 结果符合其他研究结论，并为粗糙波动率研究提供实证支持。

6. 结论

• 本文构建了一个新颖的基于Kolmogorov-Smirnov统计的分布尺度估计器，避免了传统矩方法的非线性偏差，信息利用更充分。

- 随机置换技术成功解决时间序列依赖带来的统计推断问题，通过适当技术使KS统计量有效并能推导出渐近方差。

• 无导数优化技术显著提升算法效率，易于大规模和实时应用。

- 实证发现VIX波动率平滑度显著高于实现波动率，两者均呈现远小于0.5的赫斯特指数。

• 强调分离粗糙性与长记忆的理论洪流尚未被解决，倡导未来模型应填补该空白。

---

三、图表深度解读

图1（页码15）—— 优化算法性能比较

描述

• 上图比较七种优化方法在不同$H$值下追踪KS统计量极小值的平均运行时间（秒，log刻度）。

- 下图展示各方法估计的$H$值分布（箱式图），比较估计的稳健性和准确度。

解读

• Grid Search耗时显著最大，计算时间超过1秒，多数其他方法约为0.01秒级，效率提升100倍以上。

- Brent和Nelder-Mead表现最好，时间最短且估计分布与GS几乎重合，说明在效率提升同时无损精度。

• 遗传算法、模拟退火虽快于GS，但波动较大。

联系文本

• 支持第4节论述，证明传统网格搜索虽稳健但不适合高密度估计。

- 鼓励采用衍生无导数算法，尤其是Brent和Nelder-Mead，在实际金融数据处理中的可行性。

---

图2（页码16）—— VIX与实现波动率赫斯特指数估计及KS统计值

描述

• 左上：VIX赫斯特指数估计结果与对应置信区间及理论正态分布。

- 右上：5分钟实现波动率赫斯特指数同上。

• 左下与右下：分别为对VIX和实现波动率计算得到的KS统计量与5%显著水平线。

解读

• VIX呈现较高且稳健的$\hat{H}$值（约0.4），置信区间较宽，且KS统计始终低于显著水平，表明模型符合假设。

- 实现波动率$\hat{H}$值较低（约0.14），同样稳定且平滑，KS统计量也未显著违反分布假设。

• 相关的正态理论分布与实证估计相符，提升了方法的信赖度。

联系文本

• 实证验证理论预测的粗糙度等级$H{\mathrm{VIX}} > H_{\mathrm{RV}}$。

- 支持第四节和第五节的实证结论，也与相关文献吻合。

---

四、估值分析

本报告无直接企业估值分析，主要为关于波动率序列粗糙度的统计方法学及其应用，无传统意义上的现金流贴现或市盈率估值内容。

---

五、风险因素评估

报告未专门列风险章节，但隐含以下风险点：

• 模型假设风险：赫斯特指数估计依赖于自相似性和分布尺度不变性假设，单路径只能检验边缘分布，联合分布假设未被检测完全，或导致推断局限。

- 置换方法的适用范围：随机置换破坏多维依赖结构，方法仅检验必要条件，不能保证过程严格自相似。

• 高频数据噪声及市场微观结构影响：尤其是实现波动率，微结构噪声与跳跃可能影响估计准确性。

- 数据质量与稳定性风险：长期跨度的VIX数据受政策变动、市场结构演化影响，可能影响估计的时间稳定性。

缓解手段包括理论证明随机置换下方差界，置信区间统计保证推断合理性，实证分段分析稳定性等，但整体仍需谨慎解释。

---

六、批判性视角与细微差别

• 统计假设限制：本文方法固然创新，但由于只检验单变量分布缩放关系而非多维分布，不能确保全程自相似性。该局限在随机置换方法的Proposition 2.5中已有明确指出。

- 随机置换与实际金融时间序列特性：置换破坏时间依赖结构，实务中可能忽略波动率的真实动态演化，故估计的粗糙度值受限于方法适用范围。

• 赫斯特指数含义的多重解读：赫斯特指数既是路径粗糙性的度量，也是长期记忆的指示，本文着重强调了两者的耦合而非分离，对模型解释带来挑战。

- 实证数据覆盖间断性及市场外因素：VIX长达35年数据，市场机制、法规变化或计算方法更新可能带来结构性变动，未在报告中详细讨论。

• 优化算法依赖问题：虽评估多算法，精度稳定，但多次仿真为基础，实盘数据的非理想性可能影响稳定性。

总体而言，报告思路清晰，理论基础扎实，对限制均有所提示，保持了较强的学术谨慎。

---

七、结论性综合

本文创新性地提出了一种基于Kolmogorov-Smirnov统计的赫斯特指数估计方法，避免了传统基于矩的偏差，采用随机置换技术，解决了金融波动率中强序列相关带来的统计推断难题，并推导了估计器的渐近方差公式，支持置信区间构建。通过多个无导数优化算法的比较，确认Brent与Nelder-Mead方法效率最高，适合大规模应用。

应用于VIX与S&P 500的5分钟实现波动率，结果表明隐含波动率的赫斯特指数约为0.40，显著高于实现波动率的0.14，确证了隐含波动率较为平滑的长久观察，这得到了严密的数学证明（Proposition 3.1）与历史文献呼应。两者均显著低于0.5，支持粗糙波动率理论，强调需将局部粗糙性与长记忆效应解耦建模这一前沿难题的重要性。

报告通过详尽的理论推导、创新实验设计与严谨的实证分析，为理解金融波动率的粗糙结构、提高相关参数估计方法的精确性和效率提供了实质贡献。

---

主要引用溯源（摘选）

• 粗糙波动率定义与历史背景：[page::0], [page::1], [page::9]

- 赫斯特指数估计方法与随机置换技术理论：[page::2], [page::3], [page::4], [page::5], [page::6], [page::7]

• 方差估计及统计推断理论推导：[page::7], [page::8], [page::9]

- VIX与实现波动率粗糙度理论比较及实证框架：[page::9], [page::10], [page::11], [page::12], [page::13]

• 优化算法对比及性能测试图1说明：[page::14], [page::15]

- 数据与实际计算结果图2说明及结论：[page::16], [page::17], [page::18]

---

附：图示引用

图1（优化算法计算时间与估计分布）


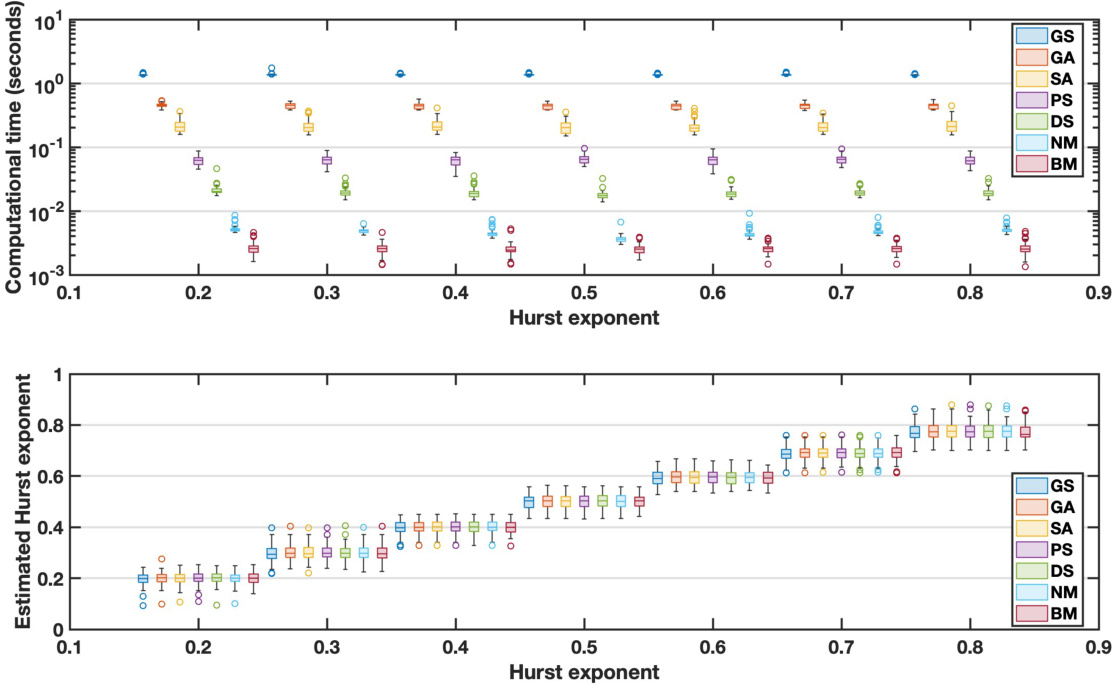
图2（VIX与实现波动率赫斯特指数估计与KS统计量）


---

综上，报告具有重要理论与实际意义，为金融波动率粗糙度的测度与理解提供了坚实的方法学基础和实证验证，值得业内与学界高度关注。

报告