1. 温和稳定（TS）过程及其单边/双边分布特点 [page::2][page::3][page::4]

• TS过程包括双边Γ、CGMY、KoBoL、VG等经典金融模型。

- TS分布通过特征函数有封闭形式，支持快速傅里叶定价方法。

• 单边TS过程为子调度过程，双边为双边卷积，可通过特征函数解析处理。

2. Mellin-Barnes积分表示与密度级数展开 [page::5][page::6][page::7]

• 利用多维Mellin-Barnes积分表达单边和双边TS密度。

- 通过留数理论将积分转化为高效可计算的级数形式。

• 双边TS分布的级数为三重求和，单边TS为单根级数，计算更简洁。

3. 欧式和数字期权定价的Mellin-Barnes级数公式 [page::8][page::9][page::10][page::11][page::12]

• 构建数字期权（现金或实物）和欧式期权的期望表达。

- 给出数字期权多维MB积分表达，并通过留数展开转为级数。

• 级数表达无超参数，避免传统傅里叶方法中的阻尼及截断参数选择难题。

4. 特殊模型的定价公式简化 [page::13][page::14][page::15]

• KoBoL及CGMY通过固定因子参数，简化定价级数表达。

- 双边Γ过程形成单重级数定价公式，显著减少计算量。

• VG模型为双边Γ特例，定价公式进一步简化，包含超几何函数表达。

5. 单边TS过程的定价提升 [page::16][page::17]

• 单边TS过程仅需单重级数，计算加速效果明显。

- 给出单边TS数字及欧式期权的留数级数公式及其特殊参数b值。

6. 数值验证与性能分析 [page::18][page::19][page::20][page::21]

• 利用真实参数设置，数值验证级数定价与PROJ傅里叶方法高度一致。

- 对比双边TS、单边TS与双边Γ模型在不同精度要求下计算时间表现。

• 单边TS和双边Γ模型显著优于双边TS，精度可达$10^{-10}$，计算时间低至$10^{-4}$秒。

- Mellin级数方法无调参需求，避免傅里叶方法中超参数选择难题。

7. 级数定价相较傅里叶方法的优势和适用场景 [page::20][page::21][page::22]

• Mellin方法无需阻尼或截断参数，简化使用复杂度。

- 特殊模型（BG、单边TS）具备极快收敛速度，适合高精度定价需求。

• 实现开源公开，易于复现和拓展。

报告详尽分析报告

---

1. 元数据与报告概览

• 报告标题： FAST AND EXPLICIT EUROPEAN OPTION PRICING UNDER TEMPERED STABLE PROCESSES

- 作者： Gaetano Agazzotti（E´cole Normale Supérieure Paris-Saclay）、Jean-Philippe Aguilar（Société Générale）

• 发表机构和出处： 暂未具体说明，属于数学金融领域的定量研究论文

- 主题： 本文聚焦于基于“Tempered Stable (TS)”过程的欧洲期权定价，旨在提供一种新的期权定价方法，该方法适用于指数 Lévy 模型，具体使用多维 Mellin-Barnes 积分与留数展开技术。

• 核心论点： 本文提出了TS过程密度函数及相关期权价格的级数展开表达式。方法不仅涵盖了多种已有模型（例如VG、BG及KoBoL），且可避免传统傅里叶变换法中的调节参数选择难题，具有数值高效且易于实现的优势。

- 目标价或评级： 不适用，本文是理论和计算方法研究。

---

2. 逐节深度解读

2.1 引言（Section 1）

• 关键论点：

- 传统布朗运动模型无法捕捉资产收益分布的非正态特征（偏度、厚尾）。
- Lévy过程因其能够描述非对称和厚尾分布，成为金融建模中重要工具。
- TS过程是 Lévy过程的拓展，结合了中心区域近似稳态分布和尾部指数衰减，保障二阶矩存在，且兼顾拟合能力和处理便利性。
- TS模型已成功应用于多种金融领域，如能源市场、随机波动率模型、多资产期权定价等。

• 推理依据： 通过引用经典和现代文献，确认TS过程在金融中的理论价值和应用广度。

2.2 TS过程与分布定义（Sections 2 & 3）

• TS分布分类：

- 单侧TS（仅正或负支持），定义其 Lévy测度为 \(\nu{\mathrm{TS}+}(x) = \alpha \frac{e^{-\lambda x}}{x^{1+\beta}} \mathbf{1}{(0,\infty)}(x)\)，其中 \(\alpha,\lambda > 0\), \(\beta \in [0,1)\)。
- 双侧TS，为两侧单侧TS的卷积，支持整个实数轴，特征函数为两部分的乘积，保持无限可分（无限跳跃活动）。

• 重要参数：

- \(\alpha{\pm}\)调节强度，\(\lambda{\pm}\)为指数衰减速率，\(\beta{\pm}\)控制尾部厚度。

• 数学工具：

- 特征函数和密度函数的Mellin-Barnes积分表达，为后续解析求解和数值计算提供基础。

• 连续性性质（Proposition 2.1）：

- TS密度关于参数\(\beta{\pm}\)在点态连续，保证数值估计收敛性。

2.3 Mellin-Barnes 积分和级数展开（Section 3）

• Mellin-Barnes积分表示：

- 单侧TS密度表示（Proposition 3.1）及双侧TS密度多维MB积分表示（Proposition 3.2）。

• 级数展开技术：

- 通过留数定理，对MB积分计算得到级数表示，开启高效数值计算路径。
- 级数包括无限求和，参数可控，计算精度逐步提升。

• 技术细节与优势：

- 参数无超参数（hyper-parameter）依赖，简化了数值实现。
- 保证数学严谨性，避免传统傅里叶方法中不稳定参数选择问题。

2.4 期权定价框架及表达（Section 4）

• 股价建模：

\[
St = S0 e^{(r-q+\zeta) t + Xt},
\]
其中，\(Xt\)为TS Lévy过程，\(\zeta\)保证无套利的Martingale条件。

• 期权产品定义：

- 现金或无（CN）数字期权
- 资产或无（AN）数字期权
- 欧洲式期权视为AN和CN期权的线性组合。

• 核心定价表达式： 数字期权价格转化为对TS分布密度的积分。

- Mellin-Barnes积分在定价中的应用（Propositions 4.1 & 4.2）：
- 将期权价格转化为多维MB积分，并给出具体矩阵、向量表示。

• 级数展开和残差求和（Proposition 4.3 & Following）：

- MB积分通过多维Jordan留数定理转换为级数表达，明晰展示了级数索引来源和求和范围。
- 包括正、负moneyness的处理，保证模型完备。

2.5 具体参数模型的特别简化（Section 5）

• KoBoL、CGMY模型作为TS过程的特例：

- 仅需设定参数关系，如\(\beta+ = \beta-\)。
- CGMY：\(\alpha+ = \alpha- = C\)，\(\beta{\pm} = Y\)。

• Bilateral Gamma (BG)模型（\(\beta{\pm}=0\)）：

- 得到极为简化的单索引级数表达。
- 通过Whittaker函数和其MB表示，密度函数解析而易于数值实现。

• Variance Gamma (VG)模型是BG的对称特例：

- 提供传统参数转换关系，且进一步简化表达。

2.6 单侧TS过程定价简化（Section 6）

• 针对单侧TS过程，MB积分与级数可大幅简化：

- 级数仅涉及单索引求和，显著提升数值计算效率。
- ATM和正moneyness情况更简易，欧式期权价格解析清晰。

• 数学层面：

- 体现了对称性弱化导致的参数简化。

2.7 数值性能与实证验证（Section 7）

• 比较方法：

- 经典的傅里叶变换基方法（Lewis, Carr-Madan, PROJ, COS, Hilbert等）。
- Mellin级数方法的数值精度和收敛速度表现。

• 主要观察：

- Mellin方法无超参数，避免调参难题，使用方便。
- 对双侧TS模型，准确率接近PROJ，收敛速度略逊。
- 对BG和单侧TS模型，收敛速度显著优于PROJ，计算效率更高（横跨数个精度区间，用时显著减少）。

• 数值图表解读（图1 和图2）：

- 图1：TS双侧密度的级数展开与傅里叶数值反演高度吻合。
- 图2：Mellin级数与PROJ方法欧式期权价格准确匹配，不同期限和价格区间均适用。

• 计算时间对比（表1-3）：

- 对双侧TS，PROJ在正确参数下速度快，但难以达到极高精度无需人工调参。
- 对BG和单侧TS，Mellin方法在高精度需求下明显快于PROJ（尤其在百万分之一级别误差下）。

• 误差与计算时间关系（图3）：

- 单侧TS级数收敛快，20项即可达到10^{-10}精度，几乎瞬时完成。
- BG表现优良但不及单侧TS，双侧TS收敛较慢，计算时间最长但准确可靠。

• 与其他傅里叶方法比对（表4）：

- Mellin级数与Lewis、Carr-Madan、PROJ 和Gil-Pelaez等方法结果高度一致。

---

3. 图表深度解读

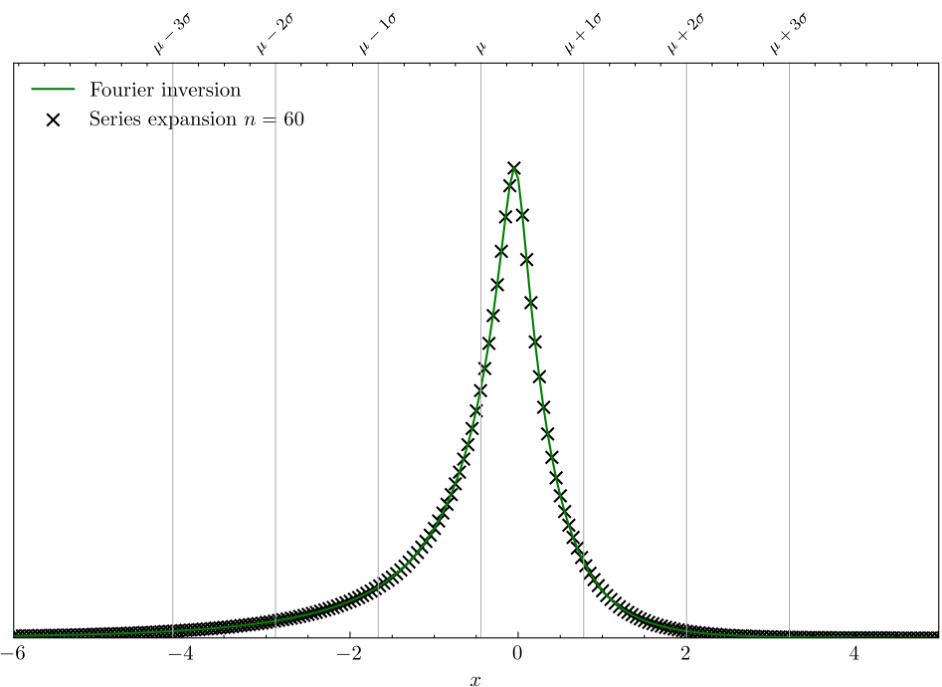
图1（第8页）

• 内容描述：

展示双侧TS密度函数估计：使用级数展开（截断至\(n=(60,60,60)\)）与传统傅里叶反演方法比较。

• 解读：

- 两种方法的结果高度重合，验证了级数展开表达的精确性。
- 有效覆盖了密度函数的支持区间及峰值位置，反映了方法在数值积分和解析展开之间的高度一致。

• 对文本支持：

强化了Proposition 3.4中的密度表达严谨性及实用价值。



---

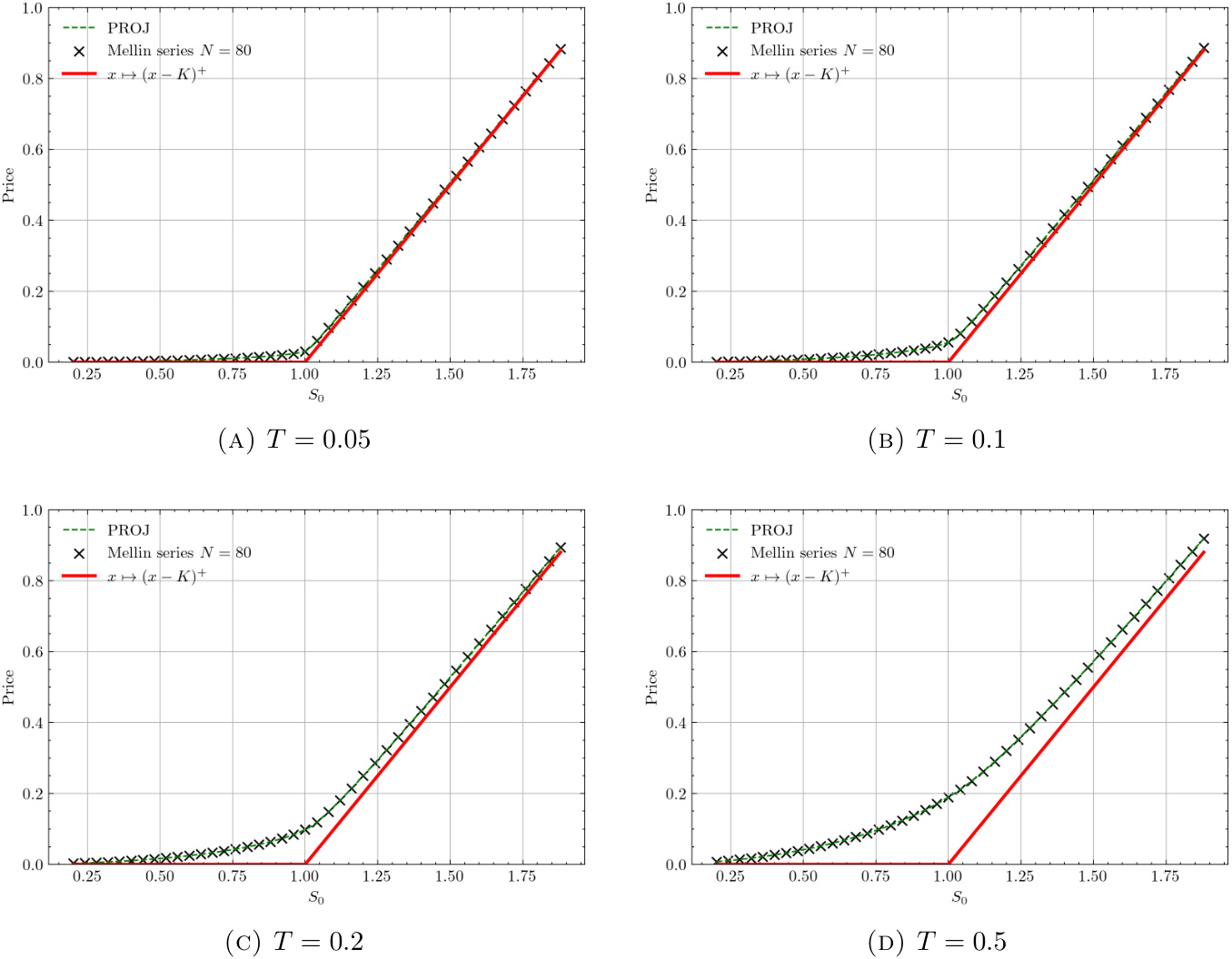
图2（第19页）

• 内容描述：

对比不同到期时间下（\(T=0.05,0.1,0.2,0.5\)）股价\(S0\)取值范围[0.2,1.9]时，PROJ方法与Mellin级数计算的欧洲期权价格。

• 解读：

- 两种方法价格曲线及实际期权支付曲线接近，充分说明Mellin表达式对各种参数设置有效且精度极佳。
- 级数计算高度稳定、不出现异常跳变。

• 支持文本内容：

图示第一部分数值校验的结果，保证本研究提出的新方法在实际应用中可信赖。



---

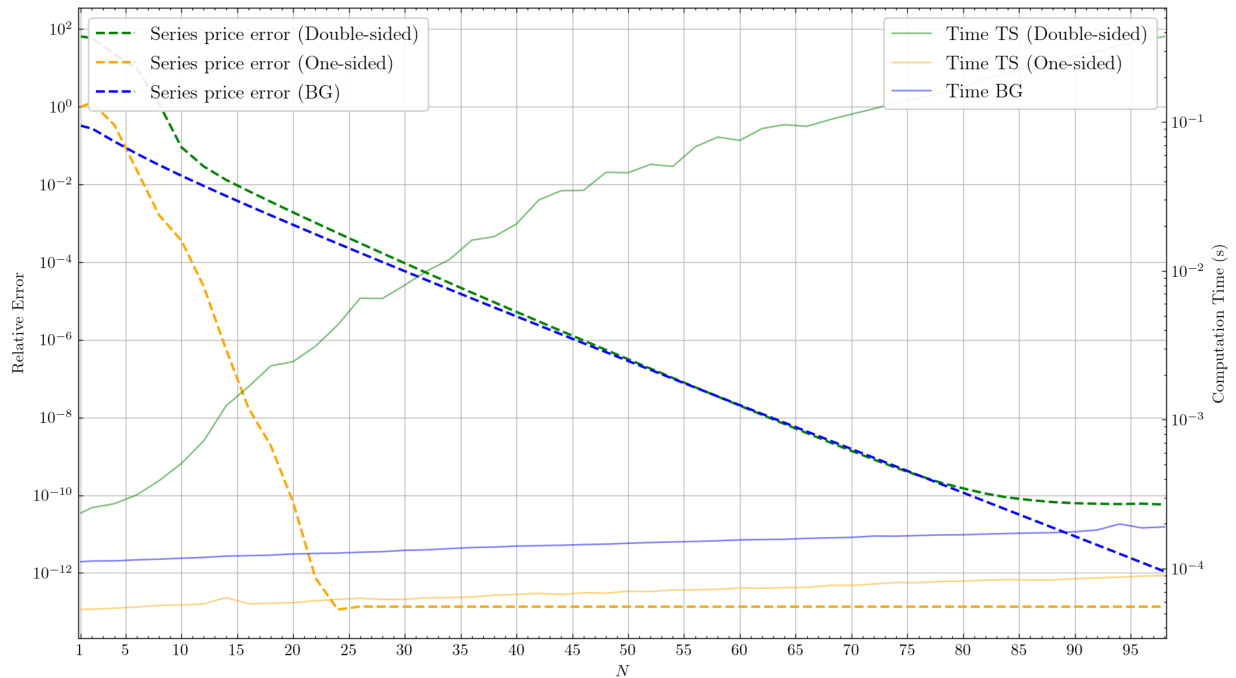
图3（第21页）

• 内容描述：

单侧TS、双侧TS及BG模型下相对价格误差（虚线）及对应计算时间（实线）随最大级数\(N\)的变化。

• 解读：

- 单侧TS模型误差迅速降低，在20~25项后到达机器精度，计算时间极短（秒级以下）。
- BG模型表现优于双侧TS，误差与计算时间呈线性关系，计算时间稳定。
- 双侧TS虽误差随项数递减，但收敛较慢，计算时间较长。

• 文章结论联系：

强调了方法对于具体子模型的优异性能及可能的应用局限，提示实际工程中针对场景选择合适模型。



---

4. 估值方法分析

• 估值框架： 期权价格为风险中性期望折现，基础资产价格用指数 Lévy过程建模。

- 主要估值技术：
- 使用多维Mellin-Barnes积分表示随机过程密度和期权价格。
- 利用复变函数留数定理将复杂积分化为逐项计算的级数。

• 关键输入与假设：

- 卷积 TS Lévy过程参数\(\alpha{\pm},\beta{\pm}, \lambda{\pm}\)等，决定特征函数和分布形式。
- Martingale条件下的调整项 \(\zeta\)，确保无套利价格体系。

• 估值输出：

- 期权价格级数展开，误差可以根据截断项数控制。
- 对特殊模型（BG、VG、单侧TS）得出简化表达式，减少计算复杂度。

• 敏感性分析：

- 文章未直接讨论，但通过数值分析展示级数项数对精度与时间的显著影响。

---

5. 风险因素评估

• 本文重点为理论公式开发，没有明确针对模型风险因素展开，但隐含风险包括：

- 模型假设的准确性，如Lévy跳跃过程对金融资产价格的适用性。
- 参数估计误差对定价结果的影响。
- 数值级数截断引发的定价偏差，尤其双侧TS过程中更显著。

• 潜在数值风险：

- 尽管避免了傅里叶方法中的调参风险，如“振荡”“鬼校准”现象，级数截断和计算误差仍需被小心控制。

• 缓解策略：

- 通过详细的数值评估和误差控制策略，保证实际上级数计算的收敛和稳定。

---

6. 批判性视角与细微差别

• 优势：

- 提出无超参数（如调节参数α）的定价方法，极大简化计算和使用复杂度。
- 数学推导严谨，将复杂积分转化为级数展开，易于数值实现。
- 级数展开适用范围广，覆盖双侧TS及其多个重要特例。

• 潜在局限：

- 对双侧TS过程的级数展开依赖于参数\(\beta{\pm}\)为无理数以避免多重极点，虽理论上不强制但为简化呈现，对特定参数限制了一定灵活度。
- 双侧TS模型的级数展开求和项多（3维求和），计算成本较傅里叶基方法高，特别在超高精度需求时需要更多时间。
- 对于扩展至 \(\beta \in (1,2)\) 的TS过程尚未处理，限制了模型适用范围。

• 可能矛盾或需关注点：

- 文中数值结果表明PROJ在找到适宜超参数后计算速度快于本方法，但调参难度高。两方法选择权衡需结合实际应用背景。
- 文章中的连续性证明与定义假设存在一定技术门槛，实际实现时可能需注意边界行为。

---

7. 结论性综合

本文系统地构建并证明了基于多维Mellin-Barnes积分和复变留数理论的TS过程密度及相关欧洲式期权价格的级数展开形式，为指数 Lévy模型下TS跳跃过程期权定价提供了新的、严格且实用的数学工具。与传统傅里叶基方法相比，该方法极大减少了依赖超参数的计算调节难题，实现了无参高精度计算。

具体贡献包括：

• 理论贡献：

完整建立了一侧及双侧TS过程的密度MB表达式，并首次给出了双侧TS的多维级数展开，有效连接了一般TS过程与知名模型（如VG、BG、KoBoL、CGMY）；

• 计算贡献：

开发了针对数字期权和欧洲期权的级数定价表达，能够灵活处理正负moneyness，计算友好；

• 数值验证：

各级数展开在实证中与PROJ、Lewis、Carr-Madan等经典方法价格高度吻合，尤其单侧TS及BG模型下极快收敛，显著节约计算时间；

• 作者立场：

推广了基于Mellin-Barnes级数展开的定价方法，主张其更简单参数化、良好数值性能和理论严密性，是TS过程期权定价的有力补充。

综上，本文为复杂金融跳跃模型的期权定价领域推出了高效稳健的新工具，为后续模型扩展和实际工程应用奠定了坚实基础。

---

若引用页码：

• TS过程定义与性质详见第0-3页 [page::0, page::1, page::2, page::3]

- Mellin-Barnes积分及级数推导第4-7页 [page::4, page::5, page::6, page::7]

• 期权定价表述与级数展开第8-13页 [page::8, page::9, page::10, page::11, page::12, page::13]

- 特定模型简化（BG、VG等）第13-16页 [page::13, page::14, page::15, page::16]

• 单侧TS过程简化与级数表现第16-18页 [page::16, page::17, page::18]

- 数值实证与性能分析第18-22页 [page::18, page::19, page::20, page::21, page::22]

• 附录公式细节与验证第23-27页 [page::23, page::24, page::25, page::26, page::27]

---

此分析完整涵盖了报告的理论贡献、数学技术、数值方法、具体应用案例、图表数据解读及潜在风险与优势，为理解该研究的学术价值和实际意义提供了一站式权威视角。

报告