模型构建与理论基础 [page::4][page::6][page::7]

• 投资组合构建关注期望收益，非精确收益预测。

- 传统基于个股特征的因子模型缺乏金融理论支持，存在过度数据挖掘风险。

• 状态变量因子模型基于资产定价理论，因子为表征经济景气的系统状态变量，风险通过个股收益与因子协方差衡量。

状态变量的筛选与风险暴露估计 [page::11][page::12][page::13][page::14][page::15]

• 初选34个宏观经济指标作为候选状态变量，涵盖经济增长、通胀、预期等方面。

- 通过相关性热力图剔除信息冗余高的指标，最终筛选剩9个较低相关性变量。

• 利用多元线性回归估计3493只股票对上述9个状态变量的风险暴露，得到描述性统计表明存在极值，后续进行极值处理。

因子风险溢价的估计与显著性检验 [page::15][page::16][page::17]

• 采用整体回归法和Fama-MacBeth回归法进行风险溢价估计和统计显著性检验。

- 两种方法均显示工业增加值当月同比、期限利差、市净率：万得全A三项变量风险溢价显著。

• 市场组合因子的风险溢价在Fama-MacBeth回归中不显著，暗示其可能并非有效系统风险因子。

系统风险因子表现与启示 [page::18][page::19][page::20]

• 月度风险溢价累计净值走势揭示因子风险溢价存在时间波动与轮动。

- 工业增加值同比因子表现较为稳定且长期提供正向风险溢价。

• 部分因子风险溢价在不同历史阶段呈现不同极性，存在风格切换现象。

- 选股时基于与状态变量协方差的因子暴露进行，理论基础扎实且解释系统性风险。

基于状态变量的因子模型 —— 长江证券研究所深度解析

---

1. 元数据与报告概览

• 报告标题：基于状态变量的因子模型

- 作者：覃川桃、鲍丰华

• 发布机构：长江证券研究所

- 报告日期：2020年7月29日

• 报告类型：专题报告 - 金融工程

- 研究主题：基于资产定价理论视角，构建与传统个股特征因子模型不同的状态变量因子模型，识别经济系统状态变量与股价风险溢价的关系，推动量化选股模型理论与实证结合。

该报告旨在深化因子模型理论，提出基于经济系统状态变量（宏观变量）而非单纯个股特征的因子模型，强调因子选择的理论基础和风险溢价的实证验证。核心结论指出工业增加值同比、期限利差和市场整体市净率等宏观状态变量具有显著风险溢价，为进一步基于系统风险暴露的选股策略提供理论依据和实证支持。[page::0,1]

---

2. 逐章节深度解读

2.1 因子模型回顾与传统个股特征模型缺陷

报告首先回顾了当前主流量化因子模型，典型形式是利用个股特征（如市值、估值指标、技术指标等）作为因子暴露(xij)，进而通过横截面回归估计因子风险溢价(fj)，预测个股期望收益。

缺陷显著：

• 缺乏理论基础：个股特征对于解释期望收益差异没有坚实的资产定价理论支撑。大量发现因子可能仅是统计上的“市场异象”或“数据挖掘”结果，存在过拟合风险，模型稳健性弱。

- 数据挖掘陷阱：随意添加个股特征变量，可能导致误检显著因子，但缺乏经济解释，模型表现难以推广。

结论倡导基于资产定价理论构建“状态变量”因子模型，提升模型的理论严谨性与实证有效性。[page::4,5]

2.2 基于状态变量的因子模型框架与理论基础

资产定价核心在于随机折现因子（SDF，m̃），股票预期收益率风险溢价由股票收益与SDF的协方差决定。SDF本身不可直接观测，但可视为若干经济状态变量（宏观变量）的线性组合：
$$ \widetilde{m} = \sum{k=1}^K bk \tilde{f}k = \mathbf{b}^\prime \tilde{\mathbf{f}} $$

进而建立风险溢价表达式：
$$ E(\tilde{r}i) - rf = \lambda^\prime \betai = \sum{k=1}^K \lambdak \beta{i,k} $$
其中$\beta{i,k}$衡量个股对各状态变量系统风险因子的暴露，$\lambdak$为相应因子风险溢价。

经典消费资本资产定价模型（CCAPM）与跨期资产定价模型（ICAPM）进一步阐明状态变量多为影响或预示经济景气的宏观指标，投资者因风险厌恶而重视这些状态变量的协方差。
具体而言：

• CCAPM：风险溢价由股票收益率与消费增长率的协方差决定。

- ICAPM：引入额外状态变量（例如货币政策、通胀预期等），使风险溢价基于股票收益率相对财富增长率和状态变量变动率的协方差。

总结，因子应定义为能表征经济系统状态和景气程度的变量，个股收益与因子的协方差测度个股系统风险大小。[page::6,7,8,9]

2.3 模型应用方法论：风险暴露与风险溢价估计

估计方法：

• 因子暴露多通过个股收益率对状态变量的多元线性回归（$\beta=\Sigma{\tilde{f}}^{-1} cov(\tilde{r}_i,\tilde{f})$）计算；

- 简单线性回归和协方差均可作为替代风险度量；

• 风险溢价通常视为自由参数，通过整体回归法或Fama-MacBeth回归法估计。

整体回归法：先估计所有股票对因子的风险暴露，再用风险暴露对股票平均收益做回归，得到因子风险溢价。

Fama-MacBeth回归：分期段横截面回归，估计每期的因子溢价，再均值化，能减少横截面相关性对统计的影响。

实证步骤包括：

• 选择合理的宏观状态变量（经济增长指标、通胀、货币政策、市场估值等）；

- 处理变量间高相关性导致的信息冗余，采用剔除或其他降维方法筛选有效变量；

• 估计个股风险暴露和因子风险溢价，检验风险溢价显著性；

- 追踪风险溢价的时间序列表现，识别风险溢价的动态变化。 [page::9,10,11]

2.4 实证分析

在34个备选宏观指标中，经过相关性分析剔除信息冗余，最终选出包括市场组合、工业增加值同比、期限利差、市净率、消费者预期指数、信用利差、PPI环比、宏观经济先行指标等9个代表指标。

• 风险暴露：根据2006年3月至2020年6月月度数据，采用多元回归法计算3493只股票的风险暴露，发现部分变量风险暴露存在极端值（需winsorize处理）。

- 相关性分析：风险暴露之间相关性较低，可直接用于回归估计。

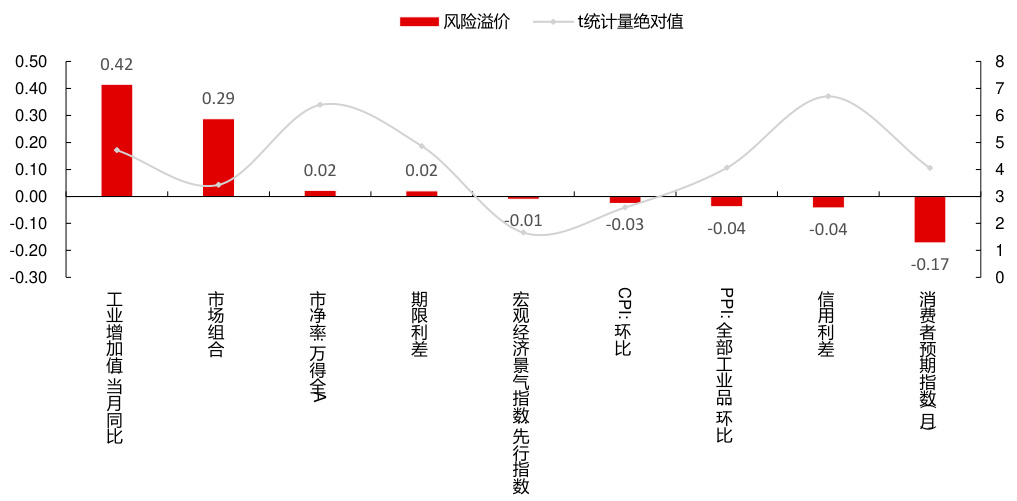
整体回归法估计结果（图4，表4）：

• 7个因子风险溢价显著，其中工业增加值同比(0.42%, t=4.71)、市场组合(0.29%, t=3.43)、市净率(0.02%, t=6.39)、期限利差(0.02%, t=4.86)正向显著；消费者预期指数、信用利差、PPI环比负向显著。

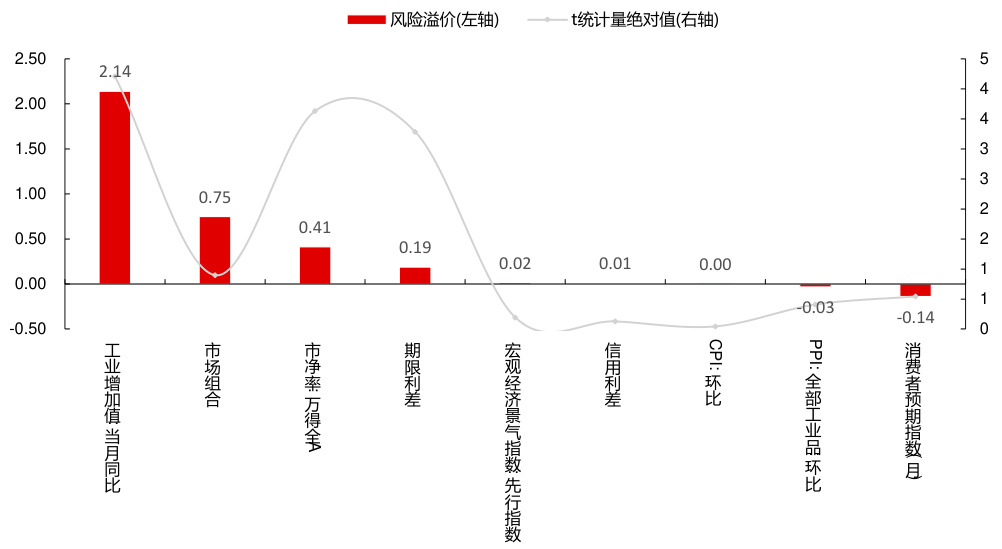
Fama-MacBeth回归（图5，表5）：

• 仅3个指标保持稳健显著：工业增加值同比（2.14%）、市净率（0.41%）、期限利差（0.19%）。

- 市场组合风险溢价虽较高但不显著，反映CAPM市场组合未必是最佳系统风险代表。

风险溢价动态表现（图6-15）：

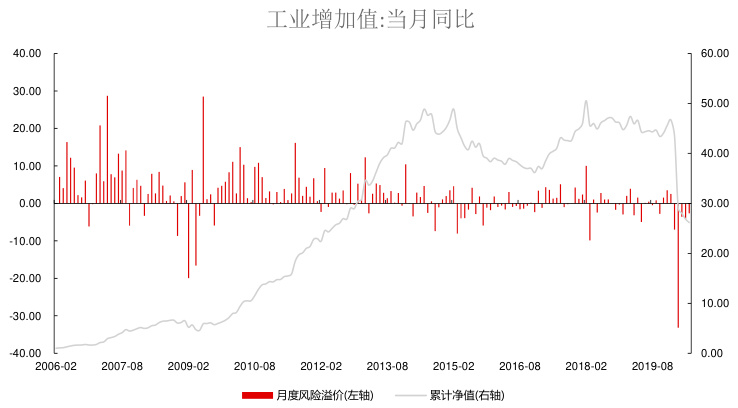
• 工业增加值同比风险溢价整体正向且在2006-2015年最显著，显示较强经济周期属性。

- 市净率风险溢价集中于2007-2009年，后期趋于平缓。

• 期限利差风险溢价在2015年后明显提升。

- 其他指标如PPI、信用利差表现出显著轮动和切换，类似传统风格因子的动态性。

该实证部分验证了基于状态变量的因子模型可识别具备显著风险溢价的系统风险变量，有助于理论和实务相结合指导选股策略设计。[page::11,12,13,14,15,16,17,18,19,20]

2.5 模型进一步思考与总结

报告提出：

• 状态变量选择：

- 状态变量应具备影响股票收益、并体现未来经济景气的能力；
- 需剔除高度相关变量，采用降维（如主成分分析）或正交化等方法进一步优化；
- 变量通常采用增量/变动率而非绝对值，以避免变量本身的强可预测性影响模型稳定性。

• 风险暴露与风险溢价估计：

- 多元回归$\beta$系数是主流方法，但数据缺失与样本非均衡问题明显；
- 可探索更多高频数据及细分收益分解方法（如隔夜收益率、日内收益率）进一步提高估计精度；
- 原始溢价的估计可以借助面板数据计量模型、PCA等先进技术提升效率与稳健性。

• 函数形式：

- 现阶段采用线性因子模型，因其统计推断便利；
- 非线性模型（机器学习等）灵活度高，但统计显著性与泛化能力检测需严格，未来研究可继续推进混合形式。

• 选股启示：

- 资产定价理论明确指出，真正影响股票期望收益的是股票与系统状态变量之间风险暴露及状态变量本身的风险溢价；
- 传统基于个股特征的因子模型虽流行，但缺乏理论支撑，易陷入数据挖掘陷阱；
- 报告实证明确工业增加值同比、期限利差和市净率等宏观变量风险溢价显著，基于这些变量构建的协方差或β系数可成为更稳健的选股基础。

综合来看，报告展示了基于状态变量的因子模型在理论自洽和实证验证上的竞争力，为量化投资提供新路径，强调通过理论指导变量筛选和实证分析实现稳健选股策略构建。[page::21,22]

---

3. 图表深度解读

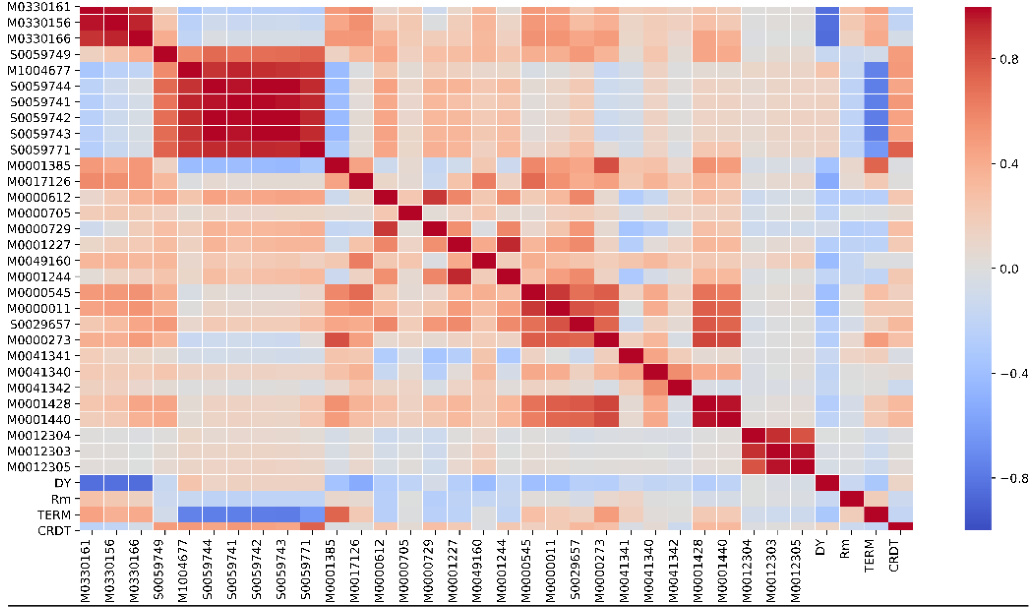
• 图1（状态变量相关系数热力图）

展示34个宏观变量间显著相关结构，如估值指标组相关度高，国债利率期限结构变量高度相关，消费物价指数以及经济景气指标存在群集相关性，说明直接使用所有变量易导致多重共线，需变量筛选。

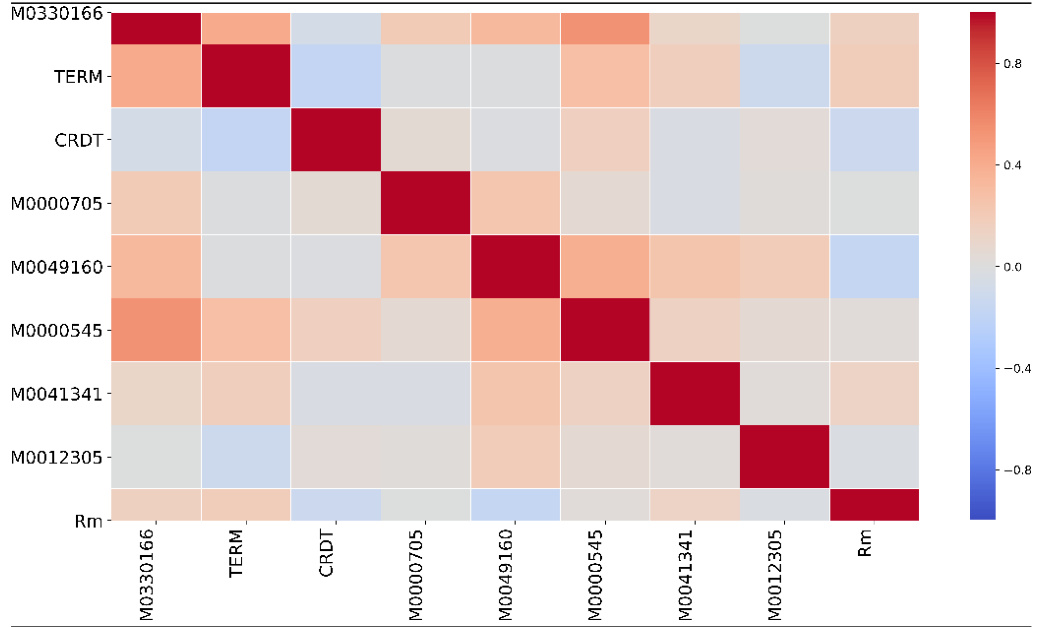
• 图2（筛选后9个变量相关系数热力图）

剔除冗余变量后，9个宏观指标相关系数均在-0.5到0.5之间，信息冗余度低，暗示统计稳健性较好。

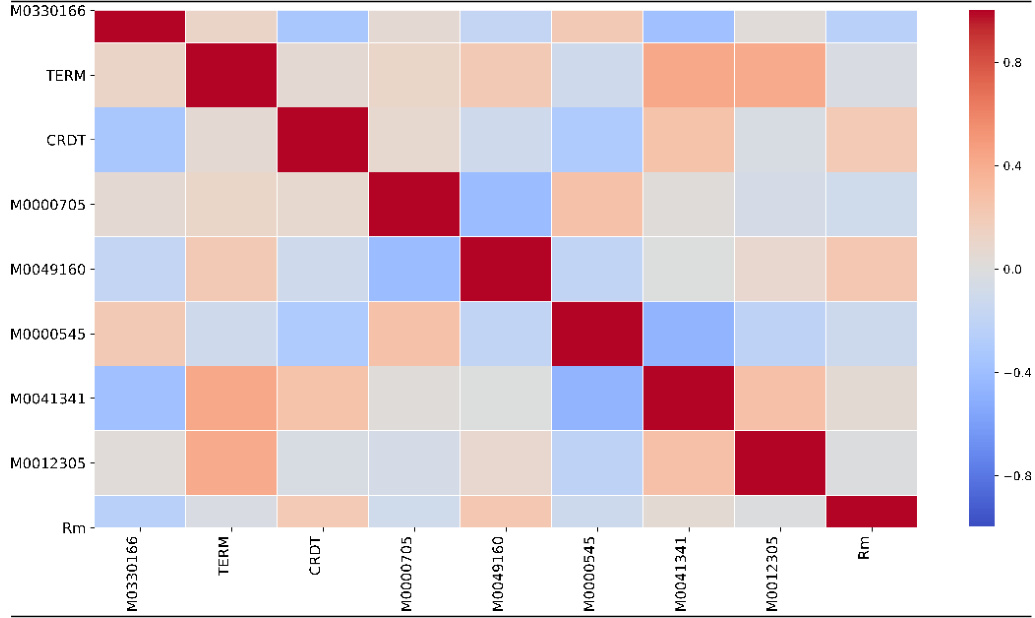
• 图3（风险暴露相关系数矩阵）

基于个股对9个状态变量的风险回归暴露，暴露间相关性低，表明个股对各宏观因子风险敏感度相对独立，有利于多因子回归的稳定估计。

• 图4（整体回归法风险溢价与t值）

红条为风险溢价数值，实线为对应t统计量绝对值，工业增加值同比、市场组合、市净率、期限利差为显著正溢价因子，消费者预期指数、信用利差、PPI环比显著负溢价因子。

• 图5（Fama-MacBeth风险溢价与t值）

与整体法相似，但风险溢价显著因子缩减为工业增加值同比、市净率、期限利差，市场组合不显著，凸显Fama-MacBeth方法在调整横截面相关性上的效用。

• 图6-15（时间序列风险溢价及累计净值）

- 如图6与图7比较，Fama-MacBeth的市场组合风险溢价走势与Wind全A指数月度收益高度一致，验证模型合理性；
- 工业增加值同比作为系统风险因子，长期呈正向累积收益趋势，体现经济周期效应；
- 市净率风险溢价主要集中于2007-2008年金融危机与其后市场波动明显；
- 期限利差风险溢价自2015年后活跃，反映货币政策转向期市场反应；
- 其他状态变量风险溢价存在轮动切换，反映风险溢价非稳态动态特征。

这些图表详细支持了报告关于状态变量风险溢价显著性及其动态变化的论述，进一步强调模型对经济因子动态解读的能力。[page::12,13,15,16,18,19]

---

4. 估值分析

报告本质为金融工程理论研发及实证，不涉及单一公司估值。其“估值”核心是基于资产定价理论推导的状态变量因子模型及因子风险溢价定量估计，使用经典线性风险溢价模型形式结合宏观数据回归实现。采用的计量方法主要为：

• 线性多元回归估计个股风险暴露$\beta$，其中$\beta$代表收益率对状态变量的敏感度；

- 整体回归与Fama-MacBeth回归估计因子风险溢价$\lambda$，体现状态变量对股票超额收益率的定价能力；

报告强调统计显著性与经济意义相结合，确立工业增加值同比、期限利差、市净率三类状态变量的估值基础。没有传统意义上DCF、P/E等估值模型的具体运用，更侧重于资产风险定价的因子识别和数据驱动的回归估价方法。[page::10,15,16]

---

5. 风险因素评估

报告识别的风险主要包括：

• 模型输入变量的选择风险：状态变量选择若不当或遗漏重要宏观因子，可能导致风险定价失真；且变量高度相关性带来的多重共线性风险可能影响回归稳定性。

- 实证方法相关风险：不同风险暴露度量方法（多元回归β、简单回归β、协方差）对于因子风险溢价结果在稳健性上有影响；Fama-MacBeth方法尽管能缓解横截面相关问题，但仍需注意截面异质性。

• 时间稳定性风险：风险溢价具有时间切换和轮动特征，部分状态变量在不同周期表现出的风险溢价波动大，模型未来效果不保证稳定持续。

- 理论与市场环境风险：模型建立在理性投资者和无套利假设之上，现实市场中行为偏差、制度变化、政策干预可能导致模型预测偏离。

缓解措施包括：合理选取状态变量，采用降维和正交化减低冗余；使用多种计量方法交叉验证；关注风险溢价的时间演变，动态调整模型参数；未来引入非线性模型提升捕捉复杂关系能力。[page::1,20,21]

---

6. 审慎视角与细微差别

• 报告在理论基础上极力强调资产定价理论对状态变量选择的指导意义，较为严谨。但现实中经济变量极度复杂和多样化，简单线性组合或许无法完全捕捉实际SDF特性，非线性关系和市场时变性可能是未来研究关键，而报告对此虽有提及但未深入探讨。

- 研究主要基于我国市场和宏观经济数据，适用性和推广性到其他市场存在不确定性，报告未明确探讨跨市场间的模型稳健性和经济结构差异。

• Fama-MacBeth回归法优势突出，但报告中风险暴露估计仍基于历史月度数据，季节性调整、结构性断点处理等细节未见充分论述，可能影响估计准确性。

- 对因子溢价的波动性及经济周期敏感性虽有描述，但对模型参数的时间一致性和对冲策略的有效性评估相对较弱。

• 由于篇幅和目标定位，报告未涉及因子模型与组合优化、机器学习等先进技术深度融合，未来提升方向明确。

整体而言，报告理论与实证结合严谨，创新地强调资产定价理论中状态变量的核心作用，提供了高质量的因子模型框架和应用示范，尚需后续深化细节与动态特性分析。[page::22]

---

7. 结论性综合

本报告从资产定价理论出发，创新构建了基于经济系统状态变量的因子模型，明确区分了传统基于个股特征因子模型缺乏理论支持和新模型的理论自洽性。实证分析发现：

• 核心状态变量：工业增加值同比、期限利差和市场整体市净率这三项宏观经济指标具有解释系统风险溢价的显著能力，能够作为稳健的风险因子。

- 风险暴露测量：通过多元回归估计个股对状态变量的风险暴露（β系数），有效度量个股系统风险承载。

• 风险溢价估计：整体回归法和Fama-MacBeth两种方法均显示上述核心因子的显著风险溢价，Fama-MacBeth法筛除噪声更有效。

- 动态表现：风险溢价存在明显轮动切换，部分因子在不同经济周期表现差异显著，类似传统风格因子。

• 模型优势：理论基础坚实，避免了传统因子模型可能出现的数据挖掘陷阱，为期望收益建模提供明确的宏观变量输入框架。

报告提出未来研究方向包括状态变量选择的降维优化、风险暴露估计的多样化方法探索、非线性函数形式的引入等，力求实现理论与实证的深度融合，以提升量化选股模型的稳健性与解释力。

综上，报告为中国乃至国际市场量化投资领域提供了一条具理论深度、实证有力的系统风险衡量新路径，推荐关注基于宏观状态变量的风险暴露作为构建稳健选股模型的核心依据。[page::1,4,6,9,11,15,16,20,22]

---

重要图表示例

1. 状态变量相关系数热力图（原始）

2. 筛选后状态变量相关系数热力图

3. 风险暴露相关系数热力图

4. 整体回归法估计风险溢价与t值（%）

5. Fama-MacBeth回归法估计风险溢价与t值（%）

6. “工业增加值:当月同比”风险溢价动态走势（%）

---

综上，报告通过严谨的资产定价理论框架结合丰富的实证分析，指出基于宏观状态变量的因子模型是衡量股票系统风险及构建稳健选股策略的重要方向，具有较强的理论与实际投资参考价值。

报告