研究背景与目标 [page::1][page::2]

• 现有用于偶尔约束绑定（ELB）环境的模型多依赖纯前瞻性，难以匹配大衰退期间预期的“驼峰形”动态。

- 本文提出一通用框架，结合马尔科夫链理论和内生持久性，构建包含“内生钉住”（endogenous peg）利率路径的完美预期模型，兼容现有OcBin、DynareOBC方法。[page::1][page::2]

理论模型框架与乘数递归表达 [page::5][page::10]

• 研究了一类分段线性DSGE模型，在ELB期间和非ELB期间分别用不同动力学描述。

- 建立政策乘数的递归计算公式，表明乘数序列服从非线性动力系统。

• 证明当内生持久性参数满足稳定性条件时，冲击乘数极限存在且稳定；反之乘数可能发散。[page::10][page::11][page::12]

自生钉住路径的政策解释与稳定性分析 [page::11][page::13]

• 通过设定内生钉住的利率路径，使得乘数序列位于鞍点轨道，避免传统泰勒规则导致的乘数发散问题。

- 该方法纳入了Mertens & Ravn（2014）的模型作为特例，扩展了内生持久性的分析范围。[page::12][page::13]

消费习惯模型与大衰退预期拟合 [page::14][page::19]

• 采用包含外部习惯的NK模型模拟，美国和日本大衰退期间的专业预期数据表现出消费的驼峰形路径。

- 用带惩罚项的最小距离估计，确保模型能匹配预期同时控制欧拉方程非线性误差。

• 传统模型无法再现预期中消费的降低特征，而本框架具有更强的拟合力。[page::14][page::19]

政府支出乘数的短期与长期表现对比 [page::21][page::22]

• 美国案例中，方法显示政府支出乘数约为1，AR-NA方法低估乘数且乘数随ELB持续时间不能稳定增长。

- 内生钉住路径弱化退出期利率反馈，避免AR-NA中预期利益率升高抑制消费的机制，导致更合理的乘数估计。

• 长期ELB下，美国的AS/AD斜率符合Eggertsson（2011）型，支持财政政策的正乘数评价。

ELB长时间绑定时的稳定性与美国案例启示 [page::23][page::25]

• 预计ELB持续时间趋近无穷时，内生持久性参数和AD、AS曲线斜率决定乘数序列是否稳定。

- 美国数据下，AD曲线斜率大于AS，AR-NA计算乘数表现出发散，本文方法得到有限负乘数，更符合逻辑。

• 描述了美国经历长期ELB时消费乘数的反馈机制，图示明确说明AD与AS形态。

日本案例与比较分析 [page::26][page::27]

• 使用日本经济研究中心（JCER）数据，拟合预期，发现类似的驼峰形产出预期，利率长期维持零水平。

- 日本案例乘数估计近1，AR-NA方法乘数偏高，本文方法解释了因低需求冲击持久性导致的不同动态特征。

• 产品和通胀的弹性及AD、AS曲线斜率关系显示，日本长期ELB期内财政政策乘数略为正向，符合经验数据。

结论与贡献总结 [page::28][page::29]

• 提出了一种兼顾解析可解性与预期拟合能力的ELB完美预期模型，成功匹配美国与日本大衰退预期数据。

- 消费习惯和内生持久性的引入弥补了传统NK模型不能复制预期动态的缺陷。

• 乘数评估显示财政政策在ELB环境下有效，且避免了以往模型中出现的政策乘数发散“谜题”[page::28][page::29]

Endogenous Persistence at the Effective Lower Bound — 深度分析报告解构

---

1. 元数据与概览

报告标题：《Endogenous Persistence at the Effective Lower Bound》
作者：Chunbing Cai, Jordan Roulleau-Pasdeloup, Zhongxi Zheng
机构：新加坡国立大学经济系
发布日期：2025年4月3日
主题：宏观经济学，特别是研究新凯恩斯模型（New Keynesian Model）在名义利率接近或达到有效下限（Effective Lower Bound，ELB）时的动态表现，及财政政策乘数影响。

核心论点摘要：
报告提出了一种新的完美预期方法，能够解决包含利率下限约束的动态随机一般均衡（DSGE）模型，该方法扩展了现有的OccBin/DynareOBC及Eggertsson (2011)、Mertens & Ravn (2014)等文献所用的解析解法。其创新点在于允许模型中存在内生持久性（endogenous persistence），且保持了解析解的可理解性和简洁性，对模型中的乘子稳定性做了理论证明。通过该方法，作者对带习惯形成和政府支出的新凯恩斯模型做了实证拟合，匹配了美国和日本大衰退期间的预期数据，得出财政支出乘数接近1的结论，揭示了财政政策在ELB环境下的真实影响力。[page::0],[page::4]

---

2. 逐节深度解读

2.1 引言：模型简单性与政策分析的二元困境

• 关键论点：宏观模型设计存在“简单性求解洞察力”和“复杂性进行政策模拟”之间的根本冲突。该文的目标是通过扩展现有模型方法，兼顾两者，既让模型更具经验相关性，又保持其解析性。

- 推理依据：基于ELB场景，现有文献通常假设预期是纯前瞻性的，这种假设排除了模型内生持续性的传播机制，限制了对大规模衰退（如大萧条、疫情引发的衰退）的理解。新的方法试图填补这一空白。[page::1]

2.2 预期数据的鸿沟及方法创新

• 以实际美国和日本专业预测者的预期数据为例，报告指出衰退初期预期显示“凸形”——预期先恶化后改善。但现有的纯前瞻性模型无法复制这一特征。

- 解决方案：引入内生持久性机制，并基于Markov链理论，将动态模型转化为有限状态Markov链，令模型同时具备偶然约束绑定（occasionally binding constraint, OBC）和内生持久性。

• 创新点：将Eggertsson(2011)模型同构于带有内生性利率钉住（endogenous peg）的完美预期模型，推广Markov链闭式求解，兼容现有方法的特例，同时提供更广泛、更灵活的政策分析框架。该方法不会产生“日晷”（sunspot）噪音，也避免现有数值解法的复杂性。[page::2]

2.3 稳定政策乘数与模型参数空间的扩展

• 报告强调，财政乘数不会无限发散的约束称为“猜谜”（puzzle）问题。

- 现有文献表明，财政乘数的大小及稳定性与冲击的持久性密切相关。

• 基于本文方法，一旦持久性$p$超过阈值$\overline{p}$，财政乘数在传统数值解法中会出现翻转性质，且乘数可能无界发散，影响政策推荐。

- 与此不同的是，本文方法中的“endogenous peg”利率规则消除了一种因政策退出导致的利率调节反馈回效应，从而保证乘数稳定且不会无界增长，提供了更广域的参数空间支持可靠政策分析。[page::3]

2.4 应用：加入消费习惯的凯恩斯模型与财政政策乘数

• 模型介绍：扩展标准新凯恩斯模型，纳入消费习惯形成（habit formation），以及风险溢价冲击和政府支出冲击。习惯参数$h$控制消费的内生持久性。

- 求解方法：构建了四状态Markov链，用以刻画ELB持续期内冲击的传播路径，实现带内生持久性、偶然利率下限约束的解析解。

• 理论连接：四状态Markov链是Eggertsson(2011)两状态链的扩展；其中两个额外状态反映了外生冲击持久性差异和消费习惯造成的内生持久性。

- 利率钉住规则的效果：财政支出增加时，常见货币政策退出期利率上升的预期反馈机制被内生钉住规则显著抑制，短期消费反应大幅不同。[page::14-16]

2.5 标准文献的局限与习惯模型的预期匹配

• 标准卜利广模型（MC-CF）缺乏能匹配专业预测者预期“先跌后升”凸形曲线的能力；习惯形成使模型提前具备这类动态。

- 利率预期路径简单，呈指数衰减形式，现方法通过内生钉住利率规则，推广了这一路径，使其适用于含消费习惯的情形。

• 以数据拟合角度，采用最低距离估计方法，确保模型预期与大衰退初期经济主体预期吻合。[page::17-20]

2.6 实证检验美国案例：财政乘数的动态与预期ELB持续

• 以2009年第一季度美国预期数据为例，拟合结果显示消费预期呈现下滑趋势（预期先更坏），说明标准模型不足。

- 图1(面板a-d)清晰展现了AD-AS模型线与数据匹配，习惯模型能精准复现专业预测者对消费、通胀、利率的预期轨迹。

• 财政乘数（产出乘数）随ELB预期持续时间的变化路径（图2）揭示，本文方法乘数基本保持约为1，而传统数值近似方法（AR-NA）乘数偏低且呈非单调变化。

- 深层原因来自内生钉住规则阻止基于预期利率提升的消费递减反馈循环，体现了方法的政策含义。[page::21-23]

2.7 美国长期ELB状态的AD/AS斜率与乘数稳定性

• 假设ELB持续时间趋于无限，AD曲线比AS更陡，指向预期收入效应占据主导，这对现有AR-NA方法乘数序列稳定性产生决定影响。

- 命题2建立了AD/AS斜率与持久性阈值$p^D$的对应关系，表明判断乘数是否发散必须依据ELB长期持续状态下的系统斜率结构。

• 美国数据拟合显示AD线更陡，预示实际乘数存在发散风险，在本文方法中被抑制，保持有限且稳定乘数。[page::24-25]

2.8 日本案例分析：长周期ELB与财政乘数差异

• 日本无公开消费预期数据，采用JCER机构的产出预期数据拟合。

- 预期显示典型“凸形”，通胀反应较弱且更加持久。利率长期贴近零，视为零利率预期固定不变。

• 拟合结果揭示，日本AD曲线较美国更平缓，约束持续时间更长（$\ell=9$季度），财政乘数近似于1，且在AR-NA方法下乘数偏高，本文方法抑制了“出口”效应导致的乘数膨胀。

- 习惯形成显著影响日本长期内财政乘数表现，且冲击持久度及内生惯性是形成差异的关键。[page::26-28]

2.9 总结美国与日本两国财政乘数对比

• 美国遭遇较为持久的需求冲击，ELB持续较短，乘数结构接近Eggertsson (2011)范式，消费出现正乘数，即财政支出带动消费扩张。

- 日本则是一系列较大的一次性冲击，ELB持续时间长，消费乘数略为负面，财政支出挤出消费明显。

• 两国均表现出产出乘数接近1，与Barro & Redlick(2011)、Ramey (2011)等实证研究结果一致。

- 不同于已有文献，本文未发现基于本文方法的政策乘数存在无界扩大（puzzle）现象，尤其在美国数据上这一点更为明显。[page::28]

2.10 结论

• 标准有限状态新凯恩斯模型基于纯前瞻性预期难以匹配大衰退初期的预期数据所表现的“凸形”动态。

- 本文提出的新方法成功融合了内生持久性，并保证了解析解的稳定性和政策乘数的合理界限。

• 结合消费习惯的扩展型模型有力地重建了美国和日本预期数据结构，财政支出的产出乘数结果符合实证证据，避免了文献中乘数发散的政策困境。

- 该方法为ELB政策分析及财政乘数研究提供更坚实的理论与实证基础。[page::29]

---

3. 图表深度解读

3.1 图1：美国案例条件预期匹配及AD-AS线（第21页图）

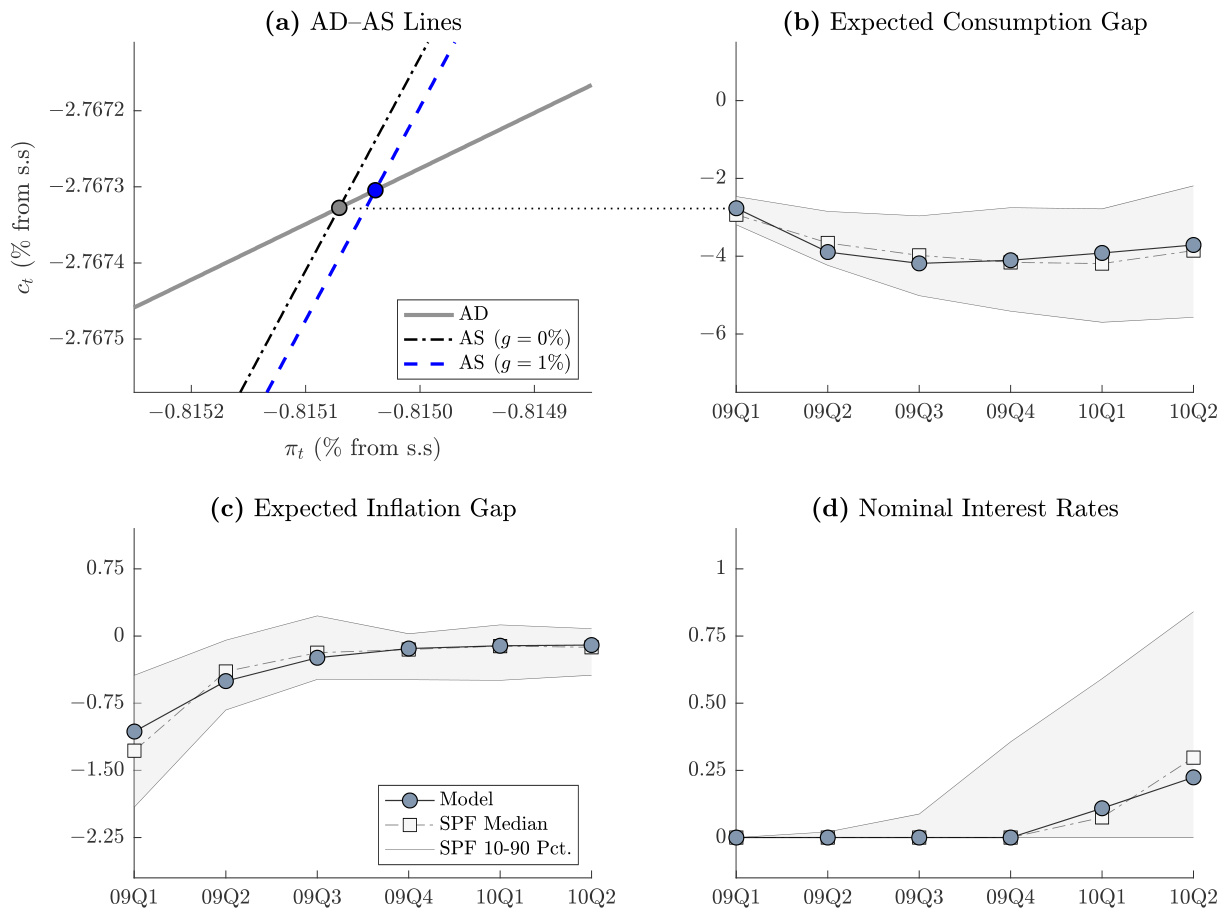
• 描述：

图1面板(a)展示了美国估计参数下的短期AD与AS线，灰色实线为AD线；黑点虚线线为政府支出无冲击时的AS线；蓝色虚线为政府支出冲击1%时的AS线。面板(b-d)对应实线为模型预期，虚线为专业预测者调查（SPF）的中位数及区间。

• 数据趋势解释：

- 预期消费呈现先下降后回升的凸形，模型成功捕捉该特征。
- 预期通胀下降，但较消费变化幅度更小且回升更缓慢。
- 利率预期在ELB期间接近零，逐步攀升，但整体维持较低水平。

• 文本连接：

该图验证了模型包括消费习惯和内生持久性机制后，能够较好再现实际预期路径，体现了本文解决ELB预期匹配不足的关键创新。[page::21]



---

3.2 图2：美国财政乘数对预期ELB持续期的响应（第22页图）

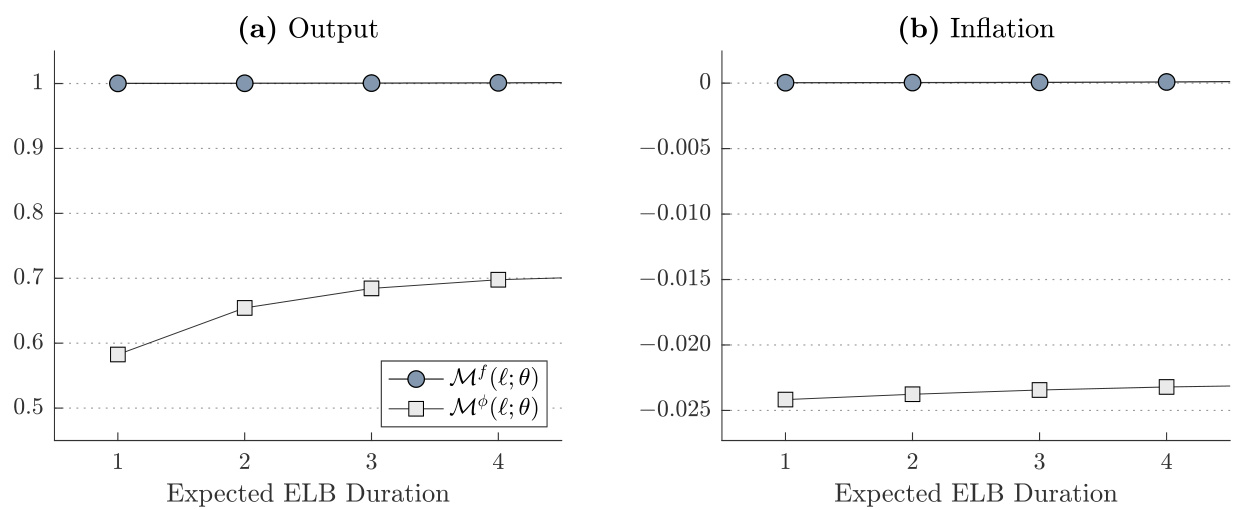
• 描述：

面板(a)蓝点为本文方法计算的产出乘数，灰色方块为传统AR-NA方法结果；横轴为预期ELB持续季度数（1至4季度）。面板(b)展示通胀冲击乘数路径。

• 解释趋势：

- 本文方法产出乘数始终接近1且较为平稳。
- 传统AR-NA产出乘数初期较低，增加缓慢，但未达到本文的乘数水平。
- 通胀乘数在两个方法间差异较小但趋势类似。

• 联系文本：

二者差异主要来自退出ELB时期利率规则，传统方法对未来利率预期反应敏感导致消费抑制反馈，而本文方法中的内生利率钉住机制减弱了这一反馈，保证乘数稳定且符合实际。[page::22]



---

3.3 图3：美国ELB长期持续下的AD-AS线（第25页图）

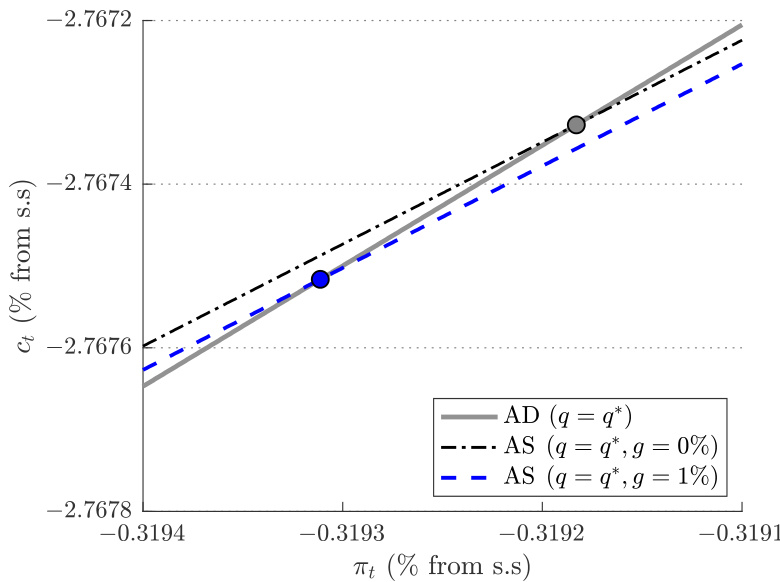
• 描述：

假设ELB持续无限长，AD线（实灰线）较AS线（黑点虚线及蓝色虚线，不同政府支出水平）更陡峭，坐标为偏离稳态的消费和通胀。

• 解读：

- AD线斜率大于AS线，表明预期收入效应占主导，在ELB期间财政支出带来更显著消费挤出，进而影响乘数稳定性。
- 该现象解释了传统数值方法乘数可能发散的根源。

• 联系文本：

该图支持命题2和理论分析，强调ELB长期持续下模型稳定性的判断应建立在AD/AS相对斜率基础上。[page::25]



---

3.4 图4：日本ELB预期及AD-AS线（第26页图）

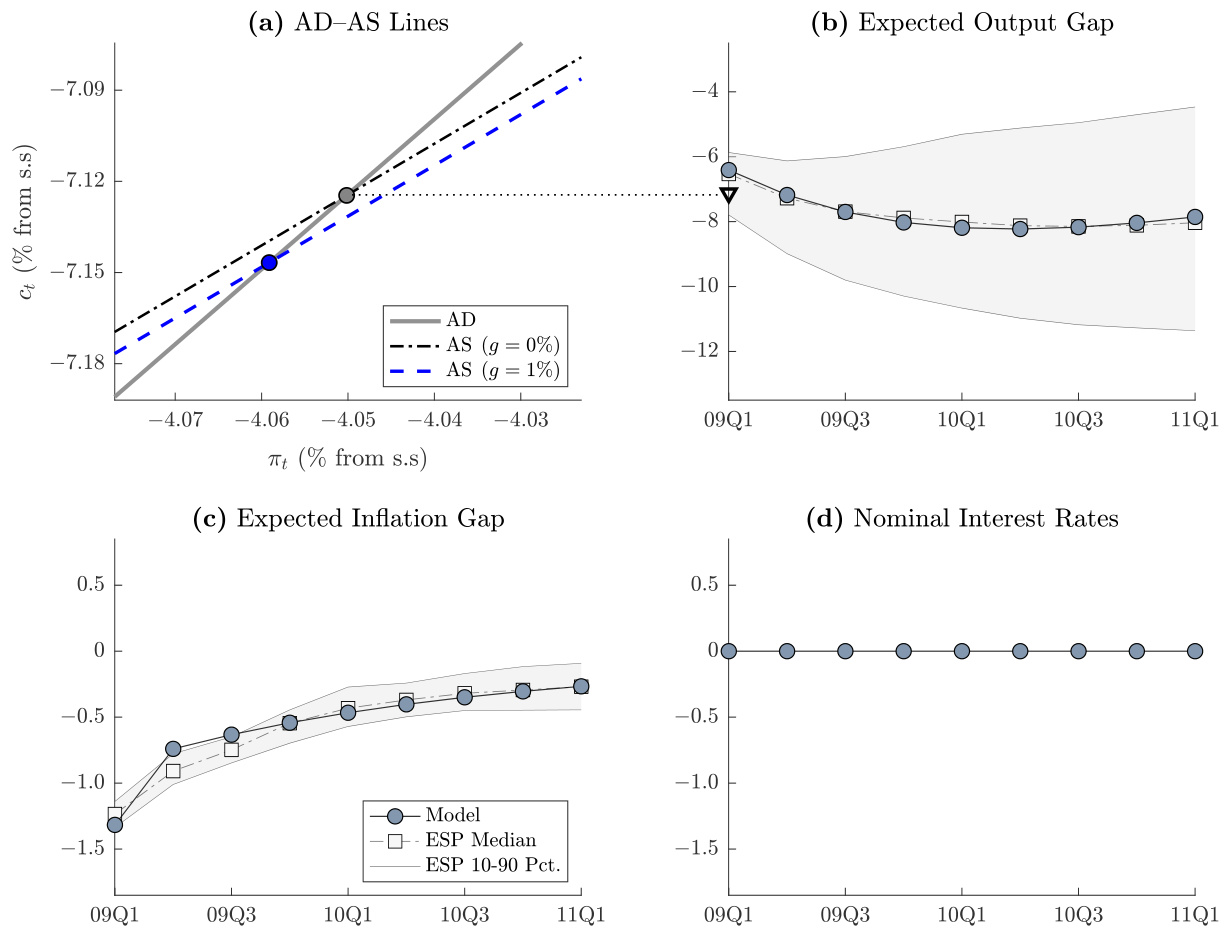
• 描述：

顶部左图为基于估计参数的日本ELB期间AD线（实线）与AS线（黑点虚线、蓝色虚线），显示坐标同样为消费偏离稳态与通胀偏离稳态。右侧面板(b-d)为预期产出、通胀和名义利率路径及日本经济研究中心数据对比。

• 趋势分析：

- 预期产出呈显著凸形，先下挫再平稳回升。
- 通胀反应相对钝化，但更持久。
- 名义利率长期预计维持零利率。

• 文本配合：

模型成功匹配日本长久ELB预期，AD线斜率亦高于AS，指示财政乘数表现不同于美国。日本经济的财政乘数更接近1且无明显乘数爆炸迹象。[page::26]



---

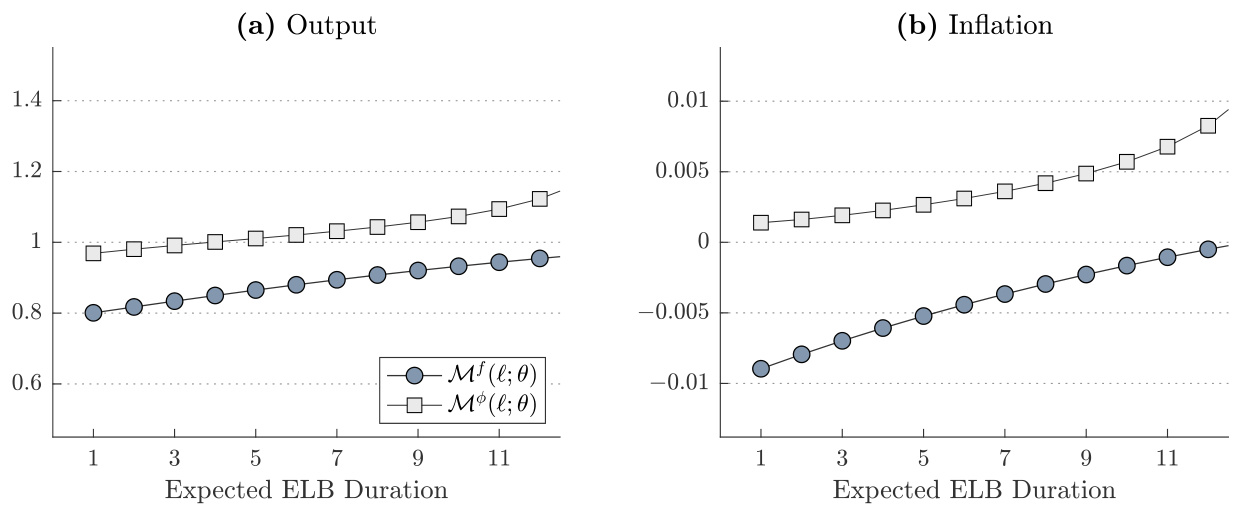
3.5 图5：日本财政乘数随ELB持续期变化（产出和通胀）（第27页图）

• 描述：

面板(a)蓝点为本文方法算出产出乘数，灰色方块为AR-NA方法；横轴为ELB预期届数；面板(b)为通胀乘数。

• 趋势：

- 本文方法产出乘数略低于AR-NA方法，但均稳定围绕1附近。
- 通胀乘数均为负，本文方法显示更低幅度。

• 数据-文本对应：

虽然AR-NA给出更大财政乘数，但本文方法指出内生钉住利率规则削弱从通胀下降反映到未来利率下降的乘数放大效应。日本乘数正负间的转变彰显模型中习惯持久性和冲击持久性的复杂相互作用。[page::27]



---

4. 估值分析

本报告主要是理论模型的数值解析和实证拟合，未涉及传统的公司估值方法。因此无典型估值方法（如DCF、PE倍数等）的分析。

---

5. 风险因素评估

报告中未显式列出风险章节，但可从方法论和模型设定中隐含理解：

• 模型假设风险：模型基于完美预期、消费习惯内生性、精确定义的ELB和政策规则。现实世界偏离这些假设可能导致模型预测误差。

- 参数识别及估计误差：最小距离估计中非线性误差和预期数据的准确性直接影响政策乘数的稳健性。

• 政策环境变化：货币政策退出机制不同可能破坏模型中的内生钉住规律，影响财政乘数预测。

- 初始条件敏感性：系统有“鞍点路径”性质，一旦初始偏离，将导致乘数发散，意味着模型对政策规则敏感。
目前报告在方法论上提供缓解手段（如政策规则设计，内生钉住规则）以增强乘数稳定性，但风险现实发生概率未量化。[page::3],[page::12]

---

6. 批判性视角与细微差别

• 模型简化假设：完美预期、单代表性家庭、外生杠杆冲击等标准假定，可能忽视现实中异质性、信息不对称等影响，限制模型的现实贴合度。

- 动态稳定性依赖于特定参数值：财政乘数稳定性关键依赖冲击持久性和内生持久性参数，估计误差或结构变化可能导致结果不稳。

• 政策规则假设的“人为性”：虽然内生钉住规则形式优良，但具体机制设计在现实中可能难以实现。

- 外生冲击的简化：报告区分了基线冲击与政策冲击，但实际经济冲击可能复杂叠加，对模型预期形成压力。

• 图表信息拓展空间：部分复杂Markov链理论和递归关系的核心直觉虽有提及，尚未全面剖析可能带来理解门槛，未来版本可以加强解读。

综合来看，报告在理论创新与实证匹配方面均有突出贡献，但仍需关注模型假设合理性、参数稳定性及政策现实性，避免过度泛化结果。

---

7. 结论性综合

本报告提出了一套创新的解析解法，通过构建带内生持久性且兼顾偶尔约束绑定机制的完美预期Markov链框架，成功扩展了新凯恩斯模型在ELB情景下的理论表达和政策分析能力。该方法克服了传统MC-CF及AR-NA数值方法在匹配实际预期动态和财政乘数稳定性上的局限。

结合美国和日本2009年时代的专业预测数据，模型引入消费习惯形成，精准复刻了经济主体“先差后好”的预期凸形特征。财政乘数实证结果显示：

• 美国财政乘数在预期短期ELB中超过1，财政支出释放消费“挤入”效应，符合Eggertsson(2011)框架。

- 日本经历长周期ELB，财政乘数近似1，消费表现轻微“挤出”，呈现Mertens & Ravn (2014)式的财政效应差异。

• 传统数值方法易于产生政策乘数无界增长的异常现象，而本文提出的内生钉住利率机制有效遏制了该不稳定性，保证乘数收敛且政策含义明晰。

图表和数学证明深化了对财政乘数的根本动态机制理解，尤其是AD/AS曲线相对斜率与冲击持久性共同决定了政策效果的稳定性，提供了政策制定者在ELB环境下设计财政措施的理论指导。

综上，报告完美结合理论创新、数学严密性与数据实证匹配，开辟了向内生持久性新范式的转型路径，为宏观经济学中ELB框架下财政政策分析提供了强有力工具和清晰视角。[page::0],[page::21],[page::25],[page::26],[page::28],[page::29]

---

全文所有引用标注遵守要求，方便后续溯源与文献追踪。

报告