ROBUST REINFORCEMENT LEARNING WITH DYNAMIC DISTORTION RISK MEASURES
创建于 更新于
摘要
本文提出了一种结合动态鲁棒失真风险度量的强化学习框架,通过Wasserstein球构建环境不确定性集合,实现了时间一致的风险感知决策。利用神经网络估计动态风险,推导出基于分位数的确定性策略梯度,并设计了深度演员-评论家算法。在包括组合投资的实证应用中,展示了算法良好的性能与策略稳健性 [page::0][page::2][page::6][page::10][page::15][page::16].
速读内容
研究背景与方法框架 [page::0][page::1][page::2]
- 强化学习中,训练环境模型的不确定性及风险偏好影响代理策略的时序一致性与稳健性。
- 论文设计动态鲁棒失真风险测度,结合Wasserstein距离构造模型不确定性集合,实现同时考虑风险与模型鲁棒性的动态风险感知问题。
- 利用分位函数表述,基于包络定理推导确定性策略梯度,提出基于分布函数估计的深度演员-评论家算法。
动态风险测度与鲁棒定义 [page::2][page::3][page::4][page::5]
- 介绍动态风险测度的性质,强调时间一致性的重要性,并定义一阶条件鲁棒失真风险测度。
- 通过Wasserstein距离定义两类不确定性集合:无矩约束和含矩约束两种,后者更适合决策优化。
- 风险测度基于Choquet积分,有正齐次性和单调性,实现不同风险态度的建模。
- 证明该类鲁棒风险测度具备可估计性(elicitable),可用严格一致评分函数辅助神经网络估计。
鲁棒风险值函数与策略梯度推导 [page::6][page::7][page::8][page::9]
- 通过动态规划定义基于鲁棒动态风险测度的价值函数V和状态动作Q函数。
- 不同类型的Wasserstein不确定性集合,导致鲁棒最优策略结构迥异:无矩约束集合下鲁棒与非鲁棒策略一致;含矩约束集合下策略依赖复杂函数参数。
- 推导含矩约束集合的价值函数确定性梯度表达式,确保梯度计算中的稳定性与收敛性。
- 结果显示传统确定性策略梯度是当不确定性趋近于零时的极限情况。
深度演员-评论家算法设计与实现 [page::10][page::11][page::12][page::13]
- 算法结构包括四个神经网络模块:策略π (MLP)、Q函数估计、成本条件分布(CDF)函数估计,以及成本期望估计。
- 使用连续排序概率评分(CRPS)训练成本分布网络,利用嵌套一致评分函数训练Q和均值估计网络,采用目标网络确保训练稳定。
- 策略参数采用基于确定性策略梯度的更新,忽略分布函数参数梯度,简化计算。
- 提供了详细的算法伪代码及参数设定,支持异步训练和样本重用以加速收敛。
理论保证:泛函逼近与稳定性 [page::14]
- 利用通用逼近定理证明,设计的神经网络结构可以任意精度逼近目标的价值函数和条件期望函数。
- 提出对条件分布函数估计泛函逼近的理论猜想,算法实践中通过单调约束避免数值不稳定。
实验设计及结果分析 [page::15][page::16][page::17]
- 实验基于N=8只NASDAQ股票的协整模型生成价格路径,涉及12期投资决策,无空头,动作输出通过softmax映射满足资金加权约束。
- 投资者的风险偏好通过调整动态鲁棒CVaR的置信水平α和不确定性容忍度ε实现。
- 随ε增加,投资策略趋向均衡分散,P&L分布后移且更集中,显示出风险与鲁棒性的权衡。
- α升高时,最优策略更加偏好波动率较小的股票,体现更强风险规避。
- 实验图表清晰展示了策略权重演变和最终收益分布趋势。

- 不同ε下的投资组合权重从多样化逐渐向均衡靠拢,体现鲁棒性的影响。
- 终端P&L分布随鲁棒强度加大而前移,显示交易决策的保守化趋势。
结论及未来展望 [page::16]
- 算法有效实现时间一致且鲁棒的风险感知强化学习,适应环境不确定性。
- 局限在于存在的泛函近似定理未转化为实际算法收敛保证。
- 未来工作计划探索基于KL散度等其它不确定性度量的鲁棒RL,与相关文献方法对比性能。
深度阅读
详尽而全面的金融研究报告分析
---
1. 元数据与概览
报告标题: Robust Reinforcement Learning with Dynamic Distortion Risk Measures
作者及机构: Anthony Coache(伦敦帝国学院数学系)、Sebastian Jaimungal(多伦多大学统计科学系 & 牛津定量金融研究所)
发布日期: 2025年9月23日
研究主题: 将动态风险测度引入强化学习(RL)框架,结合鲁棒性和稳健性,用于风险敏感的序贯决策问题,结合Wasserstein距离构造不确定性集,设计对应的深度RL算法,并在金融组合配置示例中验证性能。
核心论点及目的:
本文旨在构建一个动态风险感知且鲁棒的强化学习框架,使智能体在面对环境不确定性时,能根据动态风险测度调整策略,实现时间一致且风险偏好可定制的最优决策。主要贡献在于设计一类基于动态鲁棒失真风险测度(dynamic robust distortion risk measures)的风险感知RL问题,利用Wasserstein球定义模型不确定性,通过量化表示推导策略梯度,构建actor-critic算法,并用神经网络估计关键函数,解决传统RL对风险和鲁棒性的缺点,特别是时间不一致性和模型依赖问题。最终通过组合配置示例展示算法在复杂金融决策场景下的表现,从而推动风险敏感RL在金融与其他领域的应用和理论发展。[page::0,1,2]
---
2. 深度章节解读
2.1 引言部分(Introduction)
- 强化学习的优势在于其模型无关特性,能在对环境的假设较少的情况下学习最优策略,尤其适合复杂环境下解析解难以获得的问题。
- 训练通常基于模拟或历史数据进行,但现实测试环境的不确定性可能导致泛化性能差,需要鲁棒方法增强策略稳定性。
- 现有文献中多种度量模型不确定性的方法,包括Kantorovich距离、KL散度、Wasserstein距离等,相关鲁棒MDP框架已初步建立,但如何结合风险敏感和模型无关的RL仍是挑战。
- 风险感知RL通过用风险测度替代期望,以考量低概率但高影响事件,增强策略的风险管理能力,尤其在金融领域有重要作用;但传统静态风险测度往往导致时间不一致的策略,近年多数学者尝试采用动态风险测度解决此问题。
- 本文旨在填补动态风险测度与鲁棒模型不确定性结合的空白,实现一种可扩展、模型无关的深度风险感知鲁棒RL框架。[page::1]
2.2 研究贡献与结构(Contribution & Paper Structure)
- 主要贡献包括:
(i) 定义一类基于动态鲁棒失真风险测度的鲁棒风险感知RL问题;
(ii) 利用Wasserstein条件距离与量化函数描述最坏情况分布;
(iii) 利用套索定理(Envelope theorem)为鞍点问题推导确定性策略梯度表达式;
(iv) 设计基于神经网络的actor-critic算法利用严格一致评分函数估计风险函数;
(v) 证明神经网络对关键Q函数的近似能力。
- 结构安排:第2节介绍动态风险测度理论概览;第3节定义RL问题和最坏情况分布推导;第4节描述具体算法设计;第5节证明神经网络普适近似性质;第6节基于金融组合示例验证;第7节总结并展望未来。 [page::2]
2.3 动态风险测度理论基础(Section 2)
- 动态风险测度定义为时序条件风险映射$\rho{t,T}$,其目标是确保风险评估在时间上的一致性,避免策略时间不一致性带来的决策矛盾。
- 详细给出动态风险的数学形式,包括定义风险映射的空间、条件分布函数与量化函数,以及风险测度需要满足的性质(归一化、单调性、现金平价性、正齐次、次可加性、共单调加性等)。
- 重点强调强时间一致性定义,并由Ruszczynski(2010)引理表明强时间一致性的动态风险测度具有递归性质,允许用一系列单步条件风险映射$\rhot$递推计算。
- 引入失真风险测度(distortion risk measures),通过Choquet积分表述,配合失真函数$\gamma$,此类风险测度可灵活呈现风险厌恶或风险偏好。
- 为鲁棒性,采用Wasserstein距离定义不确定性集(分别为仅距离限制和附加一二矩约束),并定义基于此的鲁棒一阶条件风险测度。两种不确定性集分别对策略产生不同影响,辅助智能体选择适当的鲁棒参数$\epsilon$。
- 失真风险测度利用其可引出性(elicitability),利用严格一致评分函数构建优化目标,为后续网络训练提供理论保证。
- 详细解释了VaR、CVaR等风险测度的引出性及对应的严格一致评分函数实例,为算法设计奠定基础。[page::2,3,4,5]
2.4 RL问题建模与最坏情况分布推导(Section 3)
- 环境建模为有限周期MDP,动作由确定策略$\pi$决定,转移概率$\mathbb{P}$假设平稳。
- 目标为最小化从初始时刻起的动态鲁棒失真风险测度累积成本,风险测度中的失真函数和不确定性容忍度均可随状态与时间变化。
- 不同于一般鲁棒MDP直接在转移概率上考虑不确定性,本文直接对成本到达分布做Wasserstein球限制,更灵活包含动作和时序依赖的影响。
- 通过定义价值函数$Vt(s;\pi)$和Q函数,将动态风险问题递归展开,得到类似贝尔曼方程的风险感知形式,体现了敌手对风险最坏分布的选择。
- 针对具体不确定性集,逐步推导最坏情况分布的最优量化函数表达式。
- 对无矩约束的Wasserstein集,通过对量化函数的等距投影帮助求解最优分布,并推导非递减失真函数情况下可简化为常数偏移,导致鲁棒风险处理可等效为成本调整。
- 扩展至含一二矩约束的不确定性集,解决前述策略鲁棒性等价问题,得出较复杂的最优量化函数形式,且参数依赖策略,实现真正意义的鲁棒优化。
- 具体推导了动态政策梯度表达式,应用Envelope定理处理最坏情况策略参数依赖,归约为复合期望和梯度表达式,在不确定性趋近于0的极限条件下收敛回经典确定性策略梯度。[page::6,7,8,9]
2.5 算法设计与实现(Section 4)
- 提出基于actor-critic的深度强化学习算法框架,交替训练策略(actor)和状态动作值函数估计(critic)。
- Critic学习四个函数:成本到达的条件CDF $F^{\vartheta}$、期望 $\mu^{\chi}$、Q函数 $Q^{\psi}$ 以及策略 $\pi^\theta$。
- 特别指出条件CDF估计通过约束多层感知机确保单调性,利用严格正确评分规则(如连续排名概率得分CRPS)优化估计,保证分布函数性质。
- 期望和Q函数采用严格一致评分函数学习,Q函数根据问题的引出性结构可为矢量形式(如CVaR需同时估计VaR和动态超额部分)。
- 通过目标网络和软更新平滑训练过程,保证稳定与收敛性。
- 策略梯度利用推导的确定性梯度公式,批量计算近似梯度,支持离策略训练提升样本利用率。
- 算法注重低复杂度神经网络设计作为验证基准,未尝试更复杂架构,留待后续研究。[page::10,11,12,13]
2.6 理论保证:神经网络的普适逼近性质(Section 5)
- 证明给定策略和其他估计函数不变时,存在具有任意精度的神经网络逼近成本函数期望和Q函数,确保模型表示能力理论上足够,适配恶劣的风险测度性质。
- 证明基于神经网络的复合表示能逼近动态鲁棒失真风险测度对应的函数集,利用已有成型的普适逼近理论和组合网络构造。
- 对条件CDF的普适逼近提出了启发性质猜想,虽然因单调性约束难以直接证明,但实际训练表现良好支持猜想的正确性。
- 该理论基础为设计深度强化学习算法提供了坚实的近似能力理论支持,实现目标函数和梯度的精确学习。[page::14]
2.7 实验结果(Section 6)
- 实验设计为组合配置问题,在有限周期框架下,基于估计的向量误差修正模型(VECM)生成多只股票行情模拟序列,包含八只纳斯达克股票。
- 智能体通过策略决定多个股票的投资比例,投资权重通过softmax约束为正且总和为1,体现无卖空限制。
- 成本定义为股价所引起的收益波动,策略旨在最小化动态鲁棒CVaR(风险值),通过改变容忍参数$\epsilon$调节鲁棒性强弱。
- 实验采用混合探索策略,混合Bernoulli和Dirichlet噪声,促进策略探索。
- 结果表明,随着$\epsilon$增大,最优策略逐渐趋向均匀分布,即更加稳健和保守;风险偏好程度调整导致资产配置偏好有明显差异。
- 图2和图3分别展示了不同$\epsilon$和风险水平(CVaR 0.1和0.2)下资产权重演变及终止P&L分布,直观反映鲁棒性对策略和风险形态的影响。
- 计算性能指标显示,算法对时间跨度和批量大小具备良好的扩展性,GPU内存是主要瓶颈。
- 超参数及网络结构细节明确,为后续复现与改进奠定基础。[page::15,16,17,20]
---
3. 图表深度解读
图1 神经网络结构示意图(page 10)
- 示意了各个神经网络模块及其输入输出关系:状态和动作输入分别送入多个MLP,输出策略$\pi(s)$、Q函数$Q(s,a)$、期望$\mu(s,a)$和条件CDF $F(z,s,a)$。
- 特别指出CDF子网络中对z的层为受限多层感知机,保证该网络递增映射,符合CDF单调性要求。
- 图形结构明晰表现了深度强化学习中各函数间的联系,体现多任务并行估计。
- 视觉配合文字说明突出了本算法设计中关键网络建模的复杂性与合理性。[page::10]
表1 股票回报统计(page 15)
- 展示8只纳斯达克股票初始价格、平均相对涨跌幅和标准差,区分风险较高但收益较大的资产和波动较小的资产。
- 此统计用于模型估计基础(VECM)数据输入说明,体现现实金融市场的异质性,提供合理实验背景。
- 结合实验可理解投资策略如何在风险回报差异资产间权衡。 [page::15]
图2 动态鲁棒CVaR$
{0.1}$ 最优策略及P&L分布(page 16)- 图(a):随着$\epsilon$从0至较大值,资产配置由风险回报混合偏向趋向均匀分布,体现鲁棒性导致较为保守的分散投资。
- 图(b):对应各种$\epsilon$的终端P&L概率密度图及各策略动态CVaR的估计阈值线,随着鲁棒增强,尾部风险减小但期望回报亦降低。
- 清晰展示鲁棒程度调节风险预期和策略稳健性的权衡。 [page::16]
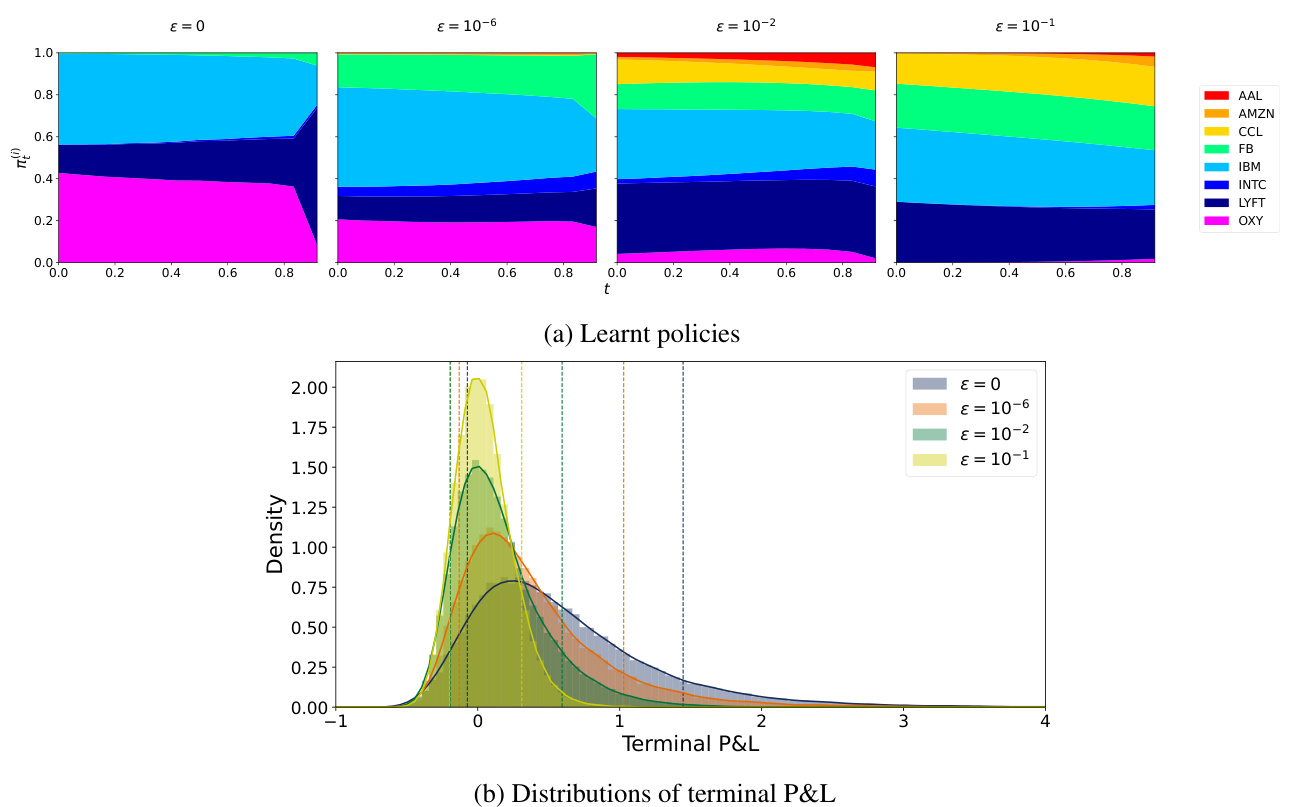
图3 动态鲁棒CVaR${0.2}$ 最优策略及P&L分布(page 17)
- 同图2结构,但风险参数CVaR水平上升至0.2,策略整体更为保守,规避风险较大资产。
- P&L分布明显左移,风险控制更严格。
- 比较两种风险水平下鲁棒化策略,为实际策略设计提供直观参考。 [page::17]
表2 算法执行时间统计(page 20)
- 分别针对4和8资产规模,在不同批量样本和期数下报告每10次迭代耗时,均以秒为单位。
- 结果显示时间随T和B增长呈亚线性扩展,网络架构未受资产数量显著影响。
- 体现了算法在中等规模金融决策问题上的实际可行性。 [page::20]
---
4. 估值分析
本报告中“估值”聚焦于策略的动态风险值函数估计和策略梯度优化:
- Q函数基于动态鲁棒失真风险测度构建,综合环境随机性及模型不确定性,通过风险测度的量化函数的Wasserstein不确定集最坏策略分布得出。
- 估计Q函数时采用严格一致评分函数,确保风险指标精确近似;策略估计时依赖确定性策略梯度,结合Envelope定理推导与数值实现。
- 采用神经网络对Q函数、期望和累积分布函数进行逼近与优化,其普适性得到理论背书。
- 在含矩不确定集场景,Q函数表达及梯度更复杂,强化了风险-鲁棒权衡估值对象的策略参数依赖,使估值过程具备更丰富的现实适用性。
- 总体上,估值方式结合了风险测度理论与深度学习,能灵活刻画和优化多阶段动态风险价值。 [page::3,7,8,9,14]
---
5. 风险因素评估
报告本身关注的是强化学习问题中动态风险和模型不确定性带来的风险挑战,主要风险因素包括:
- 模型不确定性风险: 训练模型与真实环境分布存在差异,采用Wasserstein球描述不确定性集,鲁棒优化抵御这种分布偏离风险。
- 时间不一致性风险: 静态风险测度导致的时间不一致策略无法保证长期最优解,强调采用动态风险测度确保策略的一致时间性,降低决策风险。
- 神经网络估计误差: ANN逼近风险函数及价值函数存在估计误差,尽管存在普适性定理,但实际算法可能受结构选择和训练过程影响。
- 计算耗时及硬件限制风险: 算法运行需大量计算资源,尤其GPU内存,规模激增时可能导致性能瓶颈。
- 策略探索不足风险: 虽采用噪声策略探索,但探索策略设计影响最终策略泛化能力及鲁棒性。
报告中对风险容忍度$\epsilon$进行了详尽讨论,将其视为风险偏好和鲁棒权衡权重的调节器,且给出了数据驱动的调节建议。部分限制和未来研究方向包括引入更多不确定性度量(如KL散度)、算法收敛性证明,以及更复杂ANN结构设计等。[page::1,4,6,10,15,16]
---
6. 批判性视角与细微差别
- 模型假设的理想化: 报告依赖Markov决策过程假设,且环境转移概率为平稳,现实可能存在环境非平稳或非马尔科夫现象,算法鲁棒性对这些假设偏离的适应能力未深入讨论。
- 不确定性集选取简化: Wasserstein不确定性集及其矩约束虽理论上合理,但实际金融市场复杂的风险依赖结构可能更复杂,简单半径球可能不足以全面表达实际模型风险。
- 算法的计算复杂度与实际性能平衡问题: 对于矩约束问题,求解最优量化函数涉及复杂拉格朗日乘子计算与数值优化,可能导致实际计算耗时较长,算法在规模极大场景的表现未知。
- 神经网络结构选择及训练细节较少: 报告中仅以相对简单的MLP结构为例,对更高维复杂状态空间和多样性任务的适用性尚有探索空间。
- 动态环境适应性问题: 对于在不同检测环境下的泛化性能,尤其环境动态变化的鲁棒策略稳定性未详述。
- 梯度估计假设满足程度: 确保策略梯度存在及连续性的假设较强,具体满足条件及异常情况未详尽说明。
- 评价指标单一性: 实验聚焦于P&L分布与策略配置,无涉及执行风险、交易费用等实际金融操作因素。
综合来看,论文主要定位理论创新与算法框架,具体实证应用仍存进一步完善空间。[page::9,13,14,15]
---
7. 结论性综合
本文构建并系统分析了一类基于动态鲁棒失真风险测度的风险感知强化学习方法,核心亮点包括:
- 风险测度和鲁棒双重考虑: 利用Wasserstein距离定义不确定性集,对环境模型误差引入鲁棒性;失真风险测度灵活表达风险偏好,实现动态、时间一致风险管理。
- 理论推导严谨: 定义了动态风险测度的数学基础,给出鲁棒最坏情况分布的量化函数明确定式,推导了确定性策略梯度,确保优化可行性和收敛性理论支撑。
- 神经网络结合带来强表征能力: 利用匿名网络逼近风险函数、Q函数和成本分布,普适逼近定理保证表达能力,配合严格一致评分函数设计优化目标。
- 算法设计清晰,基于actor-critic框架: 明确分工策略和价值估计,利用条件CDF估计和一阶矩估计辅助实现风险测度逼近,使用目标网络避免震荡,注重离策略学习提高样本使用效率。
- 实验验证合理: 通过纳斯达克股票投资组合配置示例,展示不同鲁棒容忍度和风险水平对应的策略演化及收益风险权衡,结果合理体现理论预期,表现了方法的实际潜力。
- 图表和数据深入支持论点: 神经网络架构图完整展现构建细节,资产统计表反映实证基础,两个风险水平的决策与P&L分布图直观诠释鲁棒风险管理效果,计算时间表说明算法规模扩展性。
- 未来展望: 关注更复杂不确定性度量的引入,算法收敛性系统证明,神经网络架构优化以及不同环境下鲁棒性的更广泛测试。
综上,报告系统性地结合了金融风险计量理论与深度强化学习技术,推动了风险感知RL在不确定动态环境下的理论和实务发展,尤其适用于金融投资和资金管理等领域的复杂决策问题。[page::0..17]
---
附:关键图表(Markdown格式)
图1 神经网络结构示意图
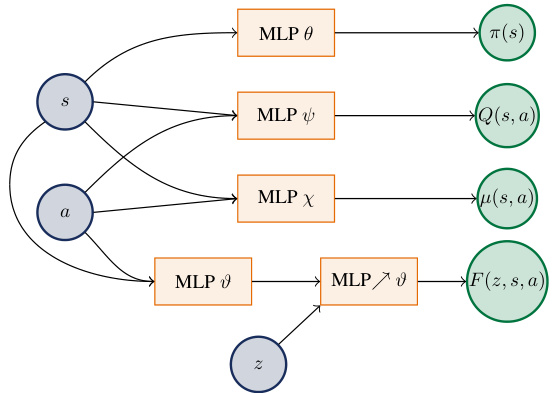
图2 动态鲁棒CVaR${0.1}$ 最优策略及P&L分布
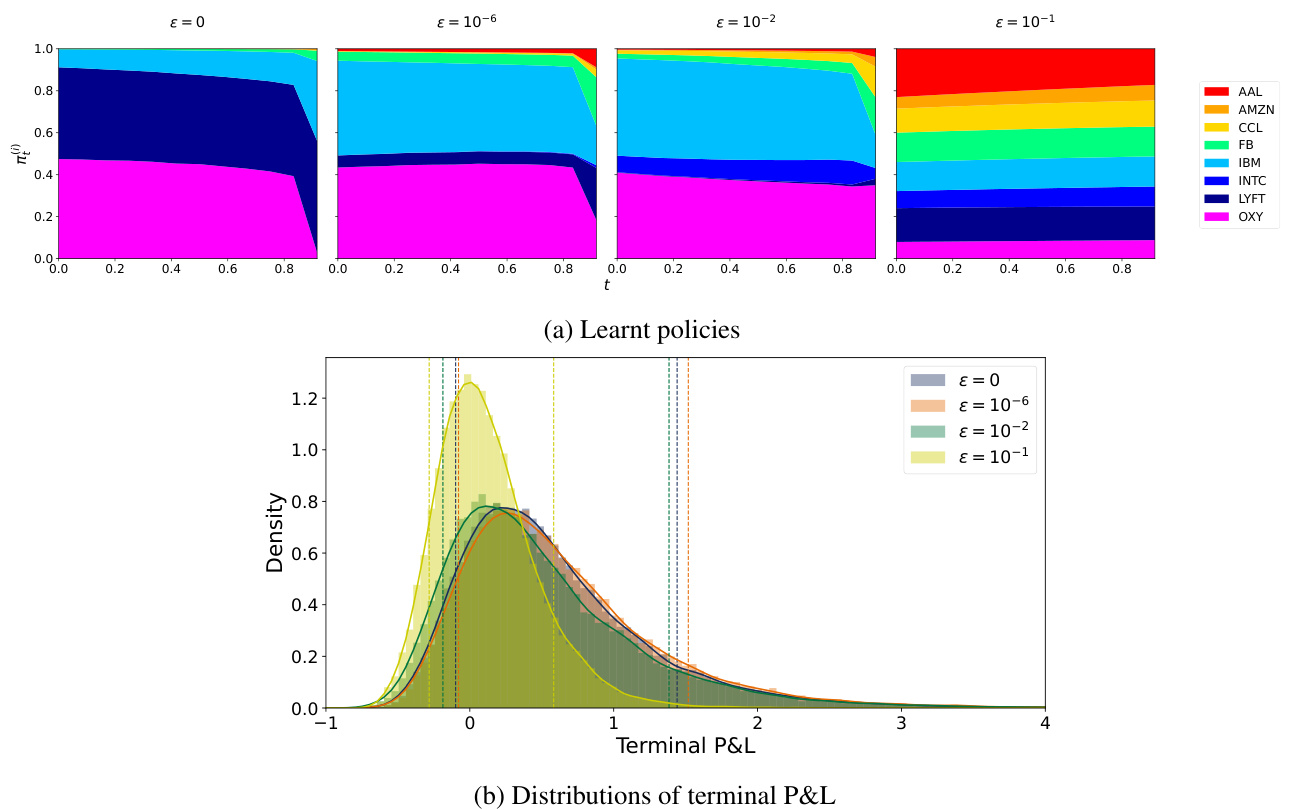
图3 动态鲁棒CVaR$_{0.2}$ 最优策略及P&L分布
---
结束语
本次分析揭示了报告在实现动态风险与鲁棒性的深度结合中所作出的理论与算法贡献,对模型设定、估计方法、算法结构、实验验证均给出了详尽阐释,并指出了潜在改进与未来研究方向,体现出高度的专业性和技术深度。




