文章背景与目标 [page::0][page::1][page::2]

• 美国式衍生品定价问题在不完全市场及信息不对称时缺乏闭式解，传统套利边界间距广泛，实用性有限。

- 本文提出基于完全动态凸风险测度的风险无差异定价框架，分别刻画买卖双方的合理价格区间，考虑双方可能不同的信息集及可实施的交易策略。

• 交易策略集合做了严格的信息适应性限制，避免卖方提前获知买方行权时间，保障策略的可实行性与信息一致性。

风险无差异价格的数学定义与无套利性论证 [page::2][page::3][page::4][page::5][page::6][page::7]

• 采用完全动态凸风险测度$\rho_{s,t}$具备单调性、现金无差异性、凸性及强时间一致性等性质构建风险函数。

- 卖方价格定义为对策略选择函数的本质下确界与买方行权时机的最大风险考量，买方价格为对行权时机及策略选择的联合最小风险值差价。

• 证明此定义的买卖价格不存在买方或卖方套利机会，确保价格体系的金融合理性。

随机波动率模型与BSDE-R-BSDE刻画 [page::9][page::10][page::11][page::12][page::13]

• 选取经典二维随机波动率模型驱动资产价格，利率常数，策略满足平方可积条件。

- 利用严格二次型驱动函数定义风险测度并通过其Fenchel对偶定义风险调整后的BSDE驱动。

• 卖方风险无差异价格表示为解BSDE-R-BSDE系统，即含带有由BSDE定义的反射边界的反射BSDE系统，体现行权后资产风险持续对风险调整价格的影响。

- 买方价格同理但反射边界及驱动取负符号差异，明确了买卖双方价格对称但不一致。

• 该系统存在唯一解，反射边界具备对行权即时风险补偿的经济诠释。

深度学习数值方法及实证分析 [page::14][page::15]

• 采用最新的反射深度向后动态规划（RDBDP）算法，结合多层神经网络与Adam优化器，离散时间步递推求解BSDE-R-BSDE系统。

- 对经典美式认沽期权，利用扭曲熵风险测度（含风险容忍度及波动风险溢价参数）的设定进行价格与隐含波动率的计算比较。

• 结果显示买卖双方价格差异较小，隐含波动率显示典型波动率笑，体现市场实际的买卖价差及美式权利价值。

- 买方美式与欧式定价结果差异较小，验证了提出模型与数值方法的有效性与实用性。

金融研究报告详尽分析报告

报告题目：Risk-indifference Pricing of American-style Contingent Claims
作者：Rohini Kumar, Frederick “Forrest” Miller, Hussein Nasralah, Stephan Sturm
发布日期：2025年9月30日
主题：美国式期权（American Options）的风险中性定价，基于完全动态凸风险度量（fully dynamic convex risk measures）和反射型BSDE（RBSDE）方法

---

1. 元数据与概览

本论文聚焦于美国式衍生品的定价问题，提出了在不完全市场和不同信息结构下，基于风险中性（indifference）定价的框架。核心贡献：

• 一般定义风险中性买卖价格（买方和卖方），允许买卖双方持有不同信息（不同滤过信息层）；

- 在随机波动率模型下，使用反射型向后随机微分方程（BSDE-RBSDE）进行风险中性价格的刻画；

• 提出基于深度学习的数值计算方法，有效解决BSDE-RBSDE系统的高维计算瓶颈。

作者通过结合现代风险度量理论和BSDE方法，解决了传统欧式选项定价方法难以有效应用于美国式选项的核心难题，尤其是在不完整市场和信息不对称的情形中，定价区间过宽且缺乏合理价位选择的问题。论文同时对买卖双方信息不对称进行了数学上的合理建模，提升模型的实用与理论价值。[page::0,1]

---

2. 逐章节深度解读

2.1 概念与市场设置

论文设定在具有完备滤过信息空间 $(\Omega,\mathcal{F},\mathbb{G},\mathbb{P})$ 的金融市场背景，包含多个风险资产和无风险资产。买方和卖方分别拥有不同信息滤过$\mathbb{F}^{buy}$与$\mathbb{F}^{sell}$，且包含资产价格过程的自然滤过。
交易策略受限于相应信息止前可预测性，禁止策略“加倍下注”。

美国式衍生品允许买方在任意适应停时点$\tau \in \mathcal{T}{0,T}^{buy}$行使，支付$\hat{\xi}\tau$。然而，不完整市场中，虽然无套利给出价格区间，但该区间往往过宽，因此需要合理的中性价格选择机制。论文采用风险中性定价，通过买或卖者在给定价格下对风险的无差异态度确定“保留价”。[page::2]

2.2 全动态凸风险度量的引入

作者采用了全动态、强时间一致性（strongly time-consistent）的凸风险度量$\rho{s,t}$，并详细列举其五个关键性质（单调性、现金不可变性、凸性、时间一致性及更强版本的时间一致性，还有$\mathcal{F}t$-正则性）。这些条件使得风险度量在不同时间动态更新且依赖于当前信息结构，较以前静态或单期风险度量模型更丰富。[page::3]

通过引入对买卖双方部分用可对冲策略减轻的风险“残余风险”定义$\hat{\rho}$和$\check{\rho}$，将风险度量有效嵌入连续交易的交易策略集合中，体现对风险的动态缓释效果。值得注意的是，残余风险的下确界可能不求得优化解，体现实际市场策略的复杂性。[page::3]

2.3 卖方价格的定义

卖方定价难点在于买方独立决定行使时间$\tau$，对卖方是未知且不可预测变量。卖方策略需根据实际行使时间适时调整，但不能事先依赖该信息，否则违背信息约束。为了捕捉该非先知性，论文创新性地引入了策略选择函数空间$\mathcal{H}'{sell}$，允许卖方策略在得知行使时间后更新，但策略对行使时间的依赖仅限于其路径表现而非随机变量本身，实现了“非先知性”并保持可预测性。并通过构造细致证明，该策略族预测性成立。[page::4,5]

对应卖方价格$P^{sell}t$通过求解卖方策略的残余风险的极小极大值再扣除无策略风险残余的基准风险值确定，公式上体现为

$$
P^{sell}t = \essinf{H \in \mathcal{H}'{sell}} \esssup{\tau\in \mathcal{T}{t,T}^{sell}} \rho{t,T}\left(\intt^T hs^\tau dSs - \xi\tau \right) - \check{\rho}{t,T}(0).
$$
该定义充分体现卖方对行使时间不确定性的防范，确保策略合理可行。[page::5,6]

2.4 买方价格的定义

买方拥有行使权，选择停时$\tau$，并选取买方信息滤过下可预测策略以降低风险。买方价格通过风险中性条件，结合最优停止与最优对冲策略下的残余风险最低点定义：

$$
P^{buy}t = \hat{\rho}{t,T}(0) - \essinf{\tau \in \mathcal{T}{t,T}^{buy}} \hat{\rho}{t,T}(\xi\tau).
$$

现金不可变性使得买方价格与初始资本无关。买方策略更直接，不涉及对卖方未知行使时间的预测，对应的策略集合简单为$\mathcal{H}{buy}$。作者还指出当买卖双方信息一致时，买卖价格差即为合理的买卖价差（bid-ask spread），且非负。[page::6,7]

2.5 无套利性质验证

定义的买、卖价格均满足无套利条件。卖方价格剖析证伪存在卖方套利可能的矛盾，类似对买方价格进行验证，均通过对冲策略的极小极大风险评估保证价格安全。值得强调，不同信息层时买卖双方策略集合不同，无买卖价跨越套利可能，仅当信息滤过一致该价格定义能互换无套利结论。[page::7,8]

2.6 与现有文献对比

论文详细回顾及评价前人基于效用函数、交易成本、指数效用、SDE效用、前向性能态指标等框架的美国式期权中性定价，指出其都基于单一信息滤过，且多数只考虑卖方策略的粗略定义。特别地，卖方策略的非预知性与策略可执行性在此前文献中多未充分讨论，本文借鉴并推广Discrete case中Kühn的策略选择方法至连续，突出了信息不对称与策略适应性的要点。部分文献的定义存在套利潜在风险。文中框架通过风险度量理论的深度整合克服了传统方法的局限，[page::8]。

3. 随机波动率模型及BSDE-R-BSDE刻画

论文专注于随机波动率模型，资产和波动率动态由两相关布朗运动驱动的SDE描述，假设参数满足正则性与有界性条件。选取的衍生品为自适应且有界的美国式期权支付过程。引入基于BSDE的全动态凸风险度量，指定驱动函数为严格二次型函数，满足一系列生长和光滑性条件，保证BSDE及反射BSDE（RBSDE）解的存在性和唯一性。

最核心结果是：

• 卖方价格可表示为BSDE-RBSDE系统的解，具体为具有自身反射边界的RBSDE，该边界本身由另一个BSDE决定（BSDE-R-BSDE）。公式框架捕捉了“行使后仍保持风险对冲”的现实情境；

- 买方价格对应类似结构，反射边界和驱动函数略有符号差异；

• 该刻画不仅理论完整，且具备数值实现基础。

此外，作者阐明了边界项为“行权价值加对零持仓的风险”，经济意义明确。若市场完整（如经典Black–Scholes模型），买卖价格一致，其对应的BSDE退化为线性方程，价差消失。[page::9-13]

---

4. 图表深度解读

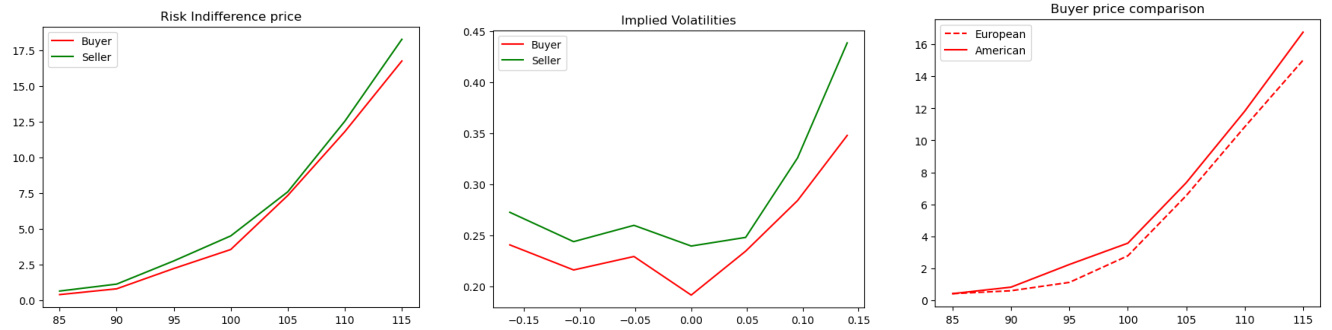
图表来自最后的数值实验部分，图示为三幅子图：

1. 左图 —— 买卖双方美国式期权的风险中性价格与执行价格关系

- 曲线呈上升趋势，反映执行价越高，期权价格越贵（看跌期权性质）。卖方价格恒高于买方价格，但差别绝对值较小，表明买卖价差有限，支持假设买卖双方风险度量相当时价格作为市场双边报价合理。

1. 中图 —— 买卖双方隐含波动率曲线（基于价格反推欧式BS价格）

- 显示典型的“微笑”特征，与市场实际波动率结构一致。卖方隐含波动率明显高于买方，说明卖方风险厌恶程度更强或价格更保守。两曲线走势较为平滑，支持随机波动率模型的适用性。

1. 右图 —— 买方欧式与美式期权价格对比

- 美式期权价格略高于欧式期权，体现提前行权权利价值，但二者差距不大，符合常见实证特征。

图表整体说明，便利的BSDE-RBSDE刻画及深度学习数值算法能够有效计算出有实际意义的风险中性买卖双边价格。此外隐含波动率曲线与已有文献（如Sircar和Sturm）结果吻合，验证了方法的正确性和鲁棒性。[page::14,15]


---

5. 估值分析与风险因素

论文基于凸风险度量和BSDE理论，估值过程本质上是求解带反射边界的BSDE系统，运用Fenchel-Young变换通过偏共轭函数（driver$g^*$）将风险度量转化为驱动函数形式。风险驱动假设明确，驱动函数严格满足二次增长与导数线性增长条件，确保BSDE求解存在唯一解。

• 关键假设包括市场资产波动率和驱动函数正则性，有界性，确保模型在理论和数值上的良好行为。

- 风险因素主要是市场不完全性（随机波动率带来的风险无法完全对冲）和信息不对称（不同的滤过信息）；模型理论上允许这些因素，且诱导不同的买卖价格差异。

• 没有在此基础上直接列出缓释策略，但通过对冲策略空间的定义隐式体现。

---

6. 批判性视角与细微差别

• 论文假定买卖双方策略分别可适应不同滤过信息，这一点充分反映现实市场信息不对称，但实际如何确定这些信息结构以及风险度量函数的具体采样还需依赖应用场景，构造具有一定理想化成分。

- 虽然模型假设较完备，但高度依赖BSDE及RBSDE理论中的正则性和技术条件，这些可能在极端市场状况下受限。

• 卖方策略定义通过策略选择函数$\mathcal{H}'_{sell}$约束合理，但该限制可能忽略市场中的部分动态反应能力或信息解读，不同现实中信息披露机制差异或导致定价偏差。

- 数值方案依赖深度神经网络和固定时间格点分割，潜在的数值稳定性与泛化能力需结合更多实证验证。

---

7. 结论性综合

本文系统地构建了美国式期权风险中性定价理论与计算框架，在不完全市场和买卖双方信息不对称背景下利用全动态凸风险度量和BSDE-RBSDE双层体系解析买卖双方的合理价格。
核心优势在于：

• 形式化定义买卖双方价格，精准处理行权时间不确定性和信息非对称；

- 用BSDE-RBSDE系统刻画价格，将风险对冲及行权风险动态整合；

• 透彻验证无套利性质，保证理论合理性；

- 融合现代深度学习算法进行数值实现，结果与经典理论和金融市场隐含波动率特征相符，具有较好的稳定性和解释力。

图表定量展现了买卖价格及隐含波动率差异，并说明美式期权权利价值较欧式期权的定量加价效应。本文既丰富了金融衍生品定价理论，也为实际应用提供切实可行的计算路径，尤其适合高维复杂模型环境下的风险评估和合理报价。

总结，作者成功地将多层风险度量、策略非预知性与数值高维计算整合，创新性地拓展了美国式期权的风险中性定价理论边界，具有较高学术价值和实践指导意义。[page::0–16]

---

总体结构参考

1. 引言与研究背景

2. 风险中性定价的理论框架及买卖双方价格定义

1. 随机波动率模型中的BSDE-RBSDE表示法

4. 数值求解方法与实证展示（深度学习方案）

1. 结论与未来展望

附录：BSDE/RBSDE存在性及最优策略理论证明

---

本分析涵盖全文主要论点、定义、理论推导与数值实验，论证严谨且结构清晰，体现极为先进的金融数学方法，堪为美国式期权风险定价研究领域的重要贡献。

报告