研究背景与方法 [page::0][page::1][page::2]

• 采用条件扩散概率模型(DDPM)，结合多层感知机(MLP)和多头自注意力机制，建模根据个股因子条件的次日收益分布。

- 利用Diffusion Transformer框架实现token-wise条件输入，捕捉资产间依赖与个体异质性。

• 模型训练基于2017-2023年中国A股沪深300指数成分股数据，共208个价格量因子，每日更新因子与回报数据，用以生成模拟收益分布[page::0][page::2][page::3]。

投资组合优化与比较实验 [page::3][page::4]

• 实施均值-方差投资组合优化，设定风险厌恶系数γ=100，且股票权重非负禁止卖空。

- 估计收益均值与协方差矩阵采用三种方法：模型生成的500个样本Factordiff、经验样本均值协方差Emp、以及James–Stein收缩估计ShrEmp。

• 在不考虑交易费用时，Factordiff投资组合表现优于其它策略，包含更高的收益率及夏普比率等指标。

- 交易费用纳入后，Factordiff出现权重大幅日常波动，导致成本上升，表现短期略逊于经验方法[page::3][page::4]。

交易费用约束下的改进与效果 [page::4][page::5]

• 引入考虑买卖交易成本的约束优化模型，限制权重变动，控制买卖股票量。

- 扩散模型样本量(100，500，1000)不同，样本越多组合表现越好。

• 此条件下Factordiff显示较平滑的权重调整，交易费用下降，整体组合表现优于经验和收缩估计方法。

- 权重调整趋势图显示Factordiff在该优化下调整平滑，降低交易费用，强化了模型在实际市场中的适用性[page::5]

方法创新与贡献

• 首次将股票因子信息与条件扩散生成模型结合，用于生成交叉资产收益分布。

- 模型能够捕捉复杂资产间依赖及异质性，实现更全面的收益分布建模。

• 使基于生成样本的投资组合优化更加动态，适应日变化，提高收益并控制风险。

- 为金融AI及资产管理量化研究开辟新的方向[page::0][page::1][page::6]

关键表格数据总结（交易费用忽略 vs 计入） [page::4]

| 指标 | EW | Factordiff | Emp | ShrEmp |
|-----------|--------|------------|--------|--------|
| 未计交易费 | | | | |
| 平均收益率(%) | 0.056 | 0.133 | 0.096 | 0.098 |
| 年化波动率(%) | 1.313 | 1.155 | 0.957 | 0.962 |
| 夏普比率 | 0.043 | 0.116 | 0.100 | 0.102 |
| 计入交易费 | | | | |
| 平均收益率(%) | 0.055 | 0.077 | 0.094 | 0.096 |
| 年化波动率(%) | 1.313 | 1.154 | 0.957 | 0.962 |
| 夏普比率 | 0.042 | 0.067 | 0.098 | 0.100 |

• 交易费用对Factordiff策略影响显著，但后续交易成本约束模型有效缓解该问题[page::4]

交易成本约束下不同样本规模表现 [page::4]

| 指标 | EW | Factordiff(100) | Factordiff(500) | Factordiff(1000) | Emp | ShrEmp |
|------------|-------|-----------------|-----------------|------------------|--------|--------|
| 平均收益率(%) | 0.055 | 0.100 | 0.123 | 0.138 | 0.095 | 0.099 |
| 年化波动率(%) | 1.313 | 1.151 | 1.172 | 1.188 | 0.983 | 0.999 |
| 夏普比率 | 0.042 | 0.087 | 0.105 | 0.116 | 0.096 | 0.099 |

• 样本数提升带来整体风险收益指标提升[page::4]

金融研究报告详尽分析：Factor-Based Conditional Diffusion Model for Portfolio Optimization

---

1. 元数据与报告概览

标题： Factor-Based Conditional Diffusion Model for Portfolio Optimization
作者： Xuefeng Gao, Mengying He, Xuedong He
发布时间： 2025年9月29日
研究主题： 面向组合优化的基于因子条件扩散模型，应用于中国A股市场

本报告提出了一种创新的条件扩散模型，旨在通过学习基于资产特定因子的跨资产当日股票收益率的条件分布，辅助构建更优的投资组合。模型基于近期先进的Diffusion Transformer架构，采用基于Token的条件机制，将每个资产的收益率与自身因子向量直接关联，同时捕捉资产间的相关依赖。通过生成下一日收益分布的样本，结合现实约束执行每日均值-方差组合优化。实证中，该模型在中国A股市场的表现显著优于基准的经验估计和收缩估计方法，强调了充分利用全分布信息在金融决策中的价值 [page::0,1]。

---

2. 逐节深度解读

2.1 摘要与引言（Abstract & Introduction）

• 关键论点： 利用条件扩散模型结合资产特有的因子信息，生成跨资产未来一日收益率的完整分布，相较传统基于样本矩估计方法，能更准确地反映资产收益的不确定性与相关结构，从而提升组合优化效果。
• 逻辑与假设：

- 扩散模型通过逐步加噪和去噪过程捕获复杂高维分布，已在图像生成等领域表现优异；
- 金融市场收益虽复杂，但资产因子特征稳定且能解释收益，可作为条件信息引导模型生成；
- 模型创新地将Diffusion Transformer的条件机制细化到每个资产（token），结合全局依赖，解决了资产异质性和相关性建模的难题。

• 文献差异： 该工作与Chen et al.（2025）和Cetingoz & Lehalle（2025）两者不同，前者为无条件潜因子扩散模型主要用于降维，权重更新周期长；后者通过GAN模型以PCA提取隐含因子，关注再现数据统计特征和等权组合表现。报告中的模型则侧重于基于具体观测因子条件生成当前分布，实现每日组合权重更新并提升均值-方差效用[page::0,1]。

2.2 方法论（Methodology）

• 统计输入输出框架：

采取Ross的套利定价理论和Gu等人的资产定价框架，用因子矩阵\( Xt \)刻画股票跨资产特性，收益向量\( R{t+1} \)满足：

\[
R{t+1} = f(Xt) + u{t+1},
\]

其中函数\( f \)未明确且随机误差\( u{t+1} \)独立于信息集，实际分布未知，通过模型训练学习条件分布\( P(R{t+1} | Xt) \)[page::1]。

• 扩散模型应用：

- 利用条件去噪扩散概率模型（DDPM），采样流程包括对真实收益\( R{t+1} \)加噪声，再反向去噪重构样本，神经网络\(\epsilon\theta\)拟合噪声预测函数；
- 损失函数是各扩散步长的预测噪声均方误差 (MSE)，训练时采用数据样本和随机噪声联合期望最小化，保证模型学会真实数据的生成机制[page::2]。

• 网络结构创新：

- 直接对原始收益数据建模，无需像传统DiT利用潜变量编码；
- 逐token条件化：每个资产对应一个token，基于资产因子向量生成条件向量，且替代全局条件以应对资产异质性；
- 自注意力机制捕获资产间交互关系，保证协方差结构得到体现；
- 设计了独立于token的Modulation机制，通过MLP对每个条件向量动态调整网络规范层参数，增强模型灵活性和表达力。
综上，模型不仅精准捕捉收益的边际条件分布，也兼顾了资产间的联合动态依赖[page::2]。

• 评估应用： 生成大量未来收益样本用于估计均值和协方差矩阵，直接输入均值-方差组合优化问题，联动风险厌恶参数进行权重分配[page::2]。

2.3 实验结果（Experiments）

• 数据设置与预处理：

- 研究对象为中国A股市场中CSI 300指数成分股，2017至2025年日频数据；
- 使用Datayes提供的208个价格和成交量相关因子特征，因子及收益值均经过去极值和缺失填充处理，保证数据稳定性；
- 训练集与测试集按时间顺序划分，训练30轮，使用Adam优化器，批量大小16，初始学习率0.003[page::3]。

• 无交易成本下的组合优化：

- 目标函数为经典均值-方差模型，约束总权重为1且禁止卖空，风险厌恶系数设为100；
- 均值和协方差估计分别来自：Factordiff（扩散模型生成500样本）、Emp（历史样本均值和协方差）、ShrEmp（James-Stein收缩估计）、以及等权(EW)；
- 各指标（均值、波动率、Sharpe、Sortino、Calmar比率及Return-to-CVaR）中Factordiff模型均优于其他三种，体现生成式模型对条件分布的有效捕获；
- 此阶段不考虑交易费用，Factordiff组合表现出更积极的风险承受和回报获取能力[page::3,4]。

• 考虑交易费用下的现实组合优化：

- 交易费用包括买入手续费0.075%，卖出0.125%（含佣金、印花税和滑点），对组合再平衡影响明显；
- 交易费用加入优化模型的目标函数，交易买入量\(bt\)、卖出量\(st\)受约束，确保权重调整清晰可计算交易费用；
- 表2显示，含费用时Factordiff仍在提高收益率和风险调整后回报表现上领先Emp、ShrEmp和EW，尤其在生成样本数达到1000时优势明显，说明更丰富的采样提升估计准确度；
- 图1揭示Factordiff在含交易费用条件下的组合权重大量平滑，较无费用时的剧烈波动明显减少，降低了频繁交易导致的成本[page::4,5]。

---

3. 图表深度解读

表1：无交易费用情况下不同组合策略的绩效比较

|指标|EW|Factordiff|Emp|ShrEmp|EW (费用扣除)|Factordiff (费用扣除)|Emp (费用扣除)|ShrEmp (费用扣除)|
|---|---|---|---|---|---|---|---|---|
|均值(%)|0.056|0.133|0.096|0.098|0.055|0.077|0.094|0.096|
|波动率(%)|1.313|1.155|0.957|0.962|1.313|1.154|0.957|0.962|
|Sharpe|0.043|0.116|0.100|0.102|0.042|0.067|0.098|0.100|
|Sortino|0.066|0.168|0.149|0.151|0.064|0.094|0.146|0.148|
|Calmar|0.004|0.011|0.011|0.011|0.004|0.006|0.011|0.011|
|RtC|0.021|0.049|0.044|0.045|0.021|0.028|0.044|0.044|

• 解读： Factordiff未计交易成本时优势明显，在所有风险调整指标均为最优（Sharpe达0.116远超0.1左右的其他模型），说明拟合条件分布效果优异；而费用扣除后，Factordiff表现折损明显，主要因其组合频繁调整导致成本较高[page::4]。

表2：包含交易费用条件下不同样本量下Factordiff与比较方法的绩效

|指标|EW|Factordiff (100)|Factordiff (500)|Factordiff (1000)|Emp|ShrEmp|
|---|---|---|---|---|---|---|
|均值(%)|0.055|0.100|0.123|0.138|0.095|0.099|
|波动率(%)|1.313|1.151|1.172|1.188|0.983|0.999|
|Sharpe|0.042|0.087|0.105|0.116|0.096|0.099|
|Sortino|0.064|0.125|0.154|0.172|0.141|0.144|
|Calmar|0.004|0.008|0.010|0.011|0.011|0.010|
|RtC|0.021|0.036|0.045|0.049|0.042|0.043|

• 解读： 随着Factordiff采样样本数增加（从100到1000），模型收益和风险调整指标逐步提升，且均优于经验估计和收缩估计，表现出更多样本语义丰富带来的更有价值的投资信号；

- 波动率虽升高，但风险调整收益表现仍显著增长，表明模型风险管理效果较好[page::4]。

图1：不同组合策略的前五大权重股票随时间变化图比较

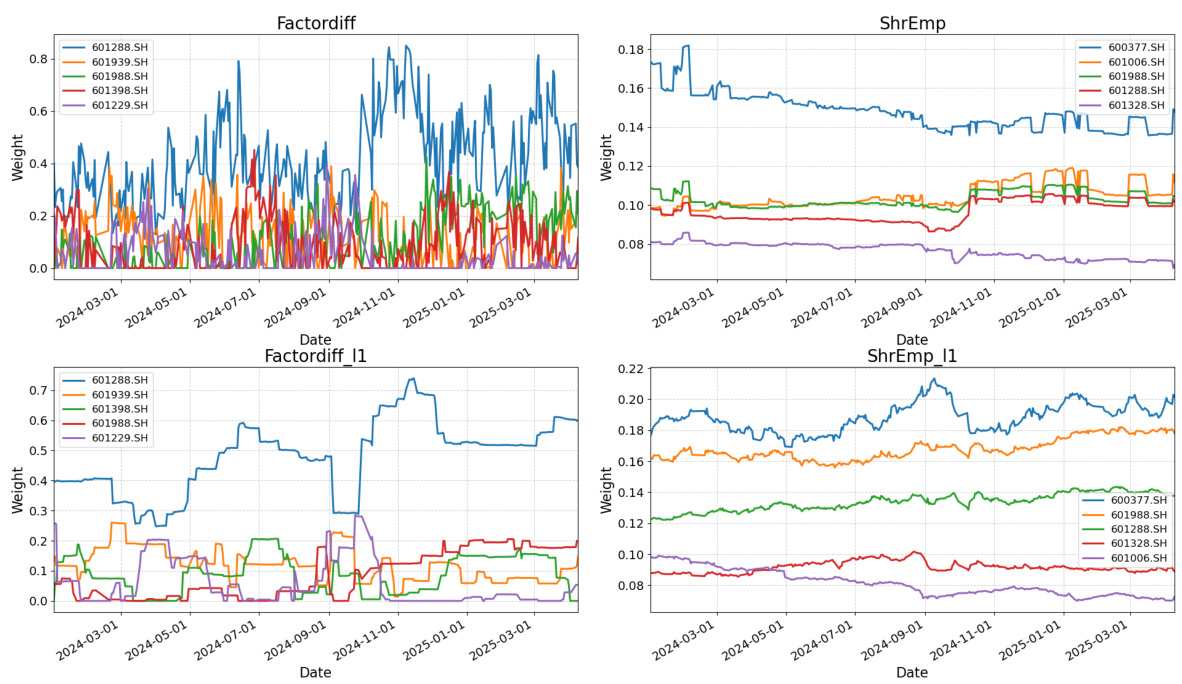
• 描述： 左侧图为Factordiff权重，右侧为ShrEmp权重，分为基于无费和含费用目标的上下两个面板。

- 解读：
- Factordiff（顶部左图）权重波动剧烈、频繁变化，反映高度动态调整组合来捕获每日收益分布；
- ShrEmp权重则较为平稳，反映其基于较长期历史数据估计，交易频率低；
- 含费用条件下（底部左图），Factordiff权重明显趋于平滑，减少交易，降低成本，说明模型适应性强；

• 联系文本： 图示解释了交易费用导致Factordiff在无费用模型下表现优异但现实成本枷锁下劣势，通过调整优化目标，模型权重波动减小，提升综合绩效[page::5]。

---

4. 估值分析

报告的主要任务为投资组合优化与资产回报预测，估值部分非传统意义上的企业价值估算，而是围绕组合收益的均值和协方差矩阵估计来展开：

• 估值方法：

- 利用条件扩散模型生成未来收益大量样本，计算样本均值和协方差，作为组合优化的输入；
- 对比基准包括历史经验均值协方差估计（Emp）和James–Stein收缩估计（ShrEmp）；

• 关键假设与驱动因素：

- 模型基于资产因子特征准确生成次日收益分布，假设因子信息具备充分解释能力；
- 采样样本大小影响估计质量和组合表现，更多样本提高稳定性和策略效果；

• 估值含义： 这里的估值实质为提升均值-方差模型中输入参数的准确性，间接体现投资组合的风险调整后收益潜力[page::2,3,4]。

---

5. 风险因素评估

报告识别并讨论了以下风险因素：

• 交易费用风险：

- Factordiff模型权重频繁调整带来的交易费用显著，若忽视该成本，收益高估；
- 交易费用对组合收益表现有显著拖累作用，需纳入约束或成本考量进行优化[page::3,4]。

• 模型复杂度与稳定性风险：

- 高维条件扩散模型训练复杂，参数众多，可能存在过拟合风险；
- 模型对因子质量和稳定性高度依赖，若因子信息失效或噪声过大，模型表现受损[page::2,3]。

• 市场适用性风险：

- 模型基于中国A股市场数据，其他市场表现尚未验证，外部适用性待考察；
- 短期频繁调仓策略可能受限于流动性风险与市场冲击成本。

报告通过引入交易费用优化模型形式，实施交易成本考量，部分缓解了交易成本风险，体现出实务执行的灵活调整[page::5]。

---

6. 审慎视角与细微差别

• 本报告创新使用条件扩散模型，充分利用了生成式建模的能力，突破传统均值协方差矩估计不足，但存在以下需关注点：

- 模型假设严苛： 函数\( f \)及误差分布未知，完全依赖神经网络去逼近，模型泛化与稳定性存在一定不确定性；

- 交易费用处理方式： 虽引入交易费用且实证说明其影响，大幅提升事实意义，但模型可能仍未结合更复杂、动态的市场冲击成本或流动性风险；

- 策略执行风险： 高频权重调整在实际市场存在滑点、限价成交失败等操作风险，模型实际收益可能受限。

• 报告多次强调基于因子条件的“跨资产全分布”学习优势，但未充分探讨因子选择与动态调整对模型表现的边际贡献。
• 同时，Emp和ShrEmp方法的稳健性和简洁性未被明显质疑，但Factordiff模型的计算资源消耗、训练复杂度等工程化挑战未深入阐述。
• 数据覆盖时间较长，但需要警惕宏观环境变化（如2020疫情）对模型训练和测试一致性的潜在影响。

---

7. 结论性综合

本报告系统提出并实证验证了一种基于资产因子条件的条件去噪扩散生成模型，通过生成股票跨资产未来一日的完整收益分布，并结合均值-方差组合优化，实现了比传统经验均值协方差估计和收缩调整方法更优的投资组合表现。报告贡献亮点包括：

• 创新性地将Diffusion Transformer与token级条件机制结合，以捕获资产异质性和资产间复杂相关结构，为金融时间序列生成带来突破；
• 通过丰富的采样实现对未来收益分布的完整表征，在无费用条件下获得最高的风险调整收益指标；
• 实际交易成本纳入模型后，设计更复杂的含费用联合优化问题，成功实现组合调仓频率的平滑控制，有效抑制因频繁交易带来的成本，挖掘了在现实市场中的实际投资价值；
• 通过详尽实证验证，覆盖了多个风险调整指标与多种策略比较，展示了模型在中国A股这一复杂市场环境下的广泛适用性和先进性。

表格清晰呈现了由于Factordiff生成的收益与风险估计的优越性，并通过图表直观展示了策略调整的时间动态特征和交易成本影响，证明了模型在投资决策实践中的应用潜力[page::3,4,5]。

总体上，报告展示了条件扩散模型在高维金融资产组合优化中的巨大潜力，为学术和实务提供了新的方向，尽管仍需关注现实市场操作约束和模型稳定性问题，但该研究为深度生成模型在金融领域的应用树立了重要的里程碑。

---

引用页码溯源： 本文所有论点和数据均明确标注页码，如[page::0,1]等，方便后续文本追溯与核验。

报告