量化CTA:Deep Momentum Network的细节思考
由crisvalentine创建,最终由crisvalentine 被浏览 402 用户
前言
传统的CTA策略多为多品种多周期的趋势跟踪策略组合。其中对于趋势的定义,大都基于时间序列计算出的传统技术指标,如MACD、均线等。然后根据趋势的多空,构建多品种的多空组合。随着深度学习的发展,很多研究者在量化CTA策略的研发中,开始尝试深度学习算法。常见的作法,如直接用深度学习预测每个品种未来一段时间的收益率,并根据预测收益构建品种多空的组合。但这钟做法有以下两个缺点:
- 直接预测收益,并没有考虑组合的风险;
- 没有考虑每个品种在组合钟的权重。
在Lim etl. 2019的论文《Enhancing Time Series Momentum Strategies Using Deep Neural Networks》中,作者提出了Deep Momentum Network(DMN)这样一个框架应用在多品种趋势跟踪策略的框架。DMN主要有以下特点:
- 直接预测N个品种未来的头寸,区间为(-1,1);
- 直接使用Sharpe比率作为模型的损失函数。
模型整体框架非常直观,输入为所有品种的特征数据,输出为所有品种下一期的信号强度,信号强度的取值区间为[-1,1],正负号表示多空的方向,数值大小表示仓位大小。其中模型部分可以采用任何用于序列预测的深度学习模型,我们这里以LSTM为例。
虽然模型非常直观,但其中有多细节值得我们推敲,我们主要讨论以下两个问题:模型怎么校准?Batch数据怎么划分等?
模型如何训练与校准?
由于模型预测的是下一期每个品种的信号强度,并不像直接预测下期收益率那样直接可以将下期收益率作为预测目标,然后再使用MSE作为损失函数。DMN最大的不同是,是直接使用Sharpe比率作为损失函数:
其中:
为所有资产在过去t-1到t-n时间平均收益, 为所有资产在过去n个时间步的方差;
为品种i在时间t+1的给组合贡献的收益率,其等于t时间计算出的信号强度 乘以组合目标波动 与品种i在过去m天的波动 ,再乘以资产i在t+1时间的收益率 。
这样,使用每个Batch的数据前向计算以上损失函数的值,再进行Backpropagation更新模型的参数,那什么时候模型停止训练呢?
这里就需要引入验证集,每次训练时,作者使用90%的数据进行训练,10%的数据用作验证集,只要满足以下任意条件,模型就停止训练:
- 达到最大的训练epoch,比如100个epoch;
- 没有达到最大的训练epoch,但在验证集上已经连续25个epoch,验证集的loss没有降低,此时就提前终止训练。
每个Batch的数据怎么准备?
根据上述损失函数的定义,每次前向计算的损失为过去N天,多品种组合表现的夏普比率的负数,所以每个Batch的数据需要支持计算出每个资产在过去N天每天的信号强度 。基于这样的需求,每个Batch的数据就不能随机抽取。以下是公众号根据本文的损失函数构造,推测的Batch数据的格式(作者在原文钟并没有提到这些细节),其中假设使用的模型为LSTM:
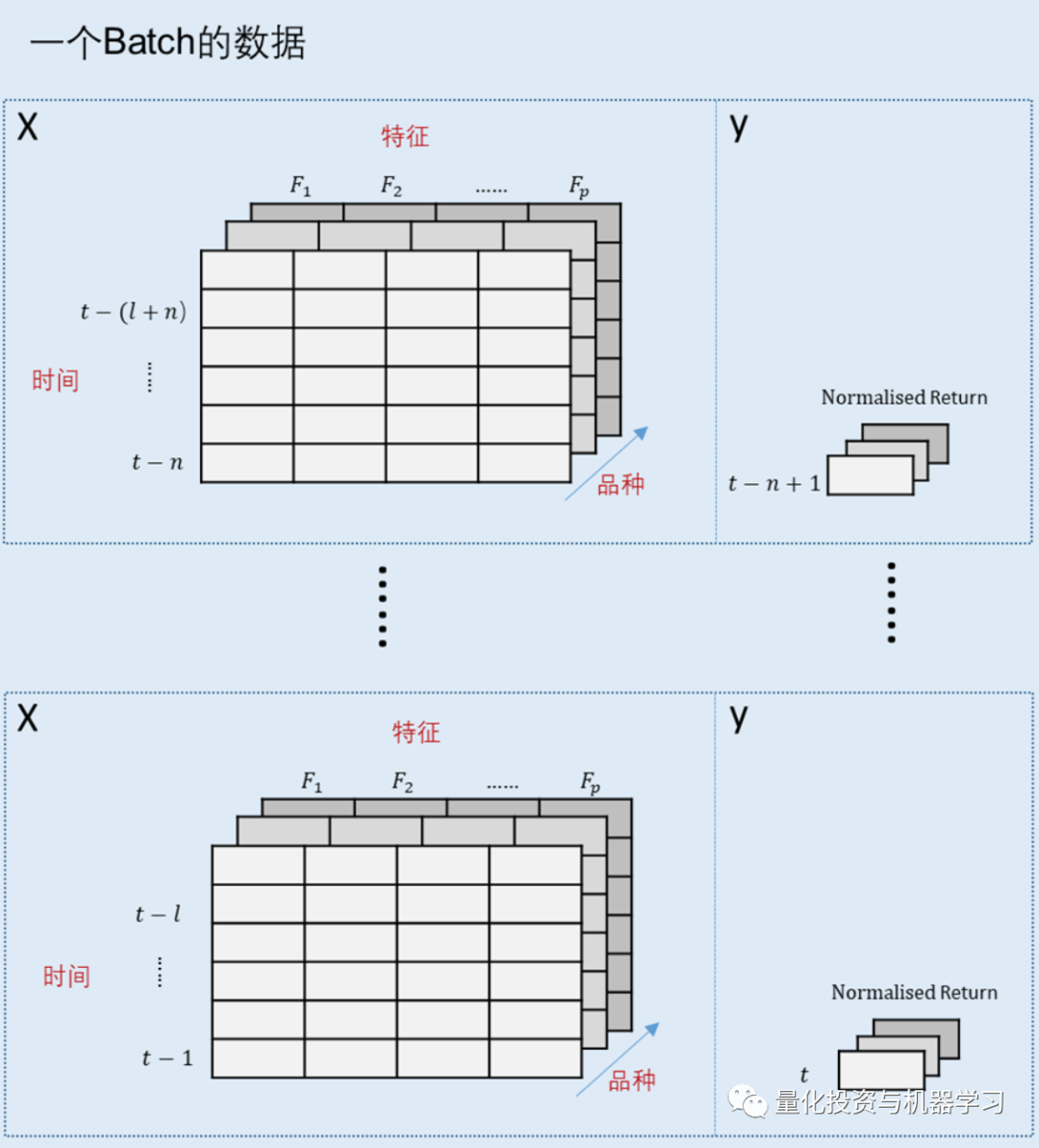
- 每个训练数据样本包括所有品种在t-n到t-(l+n)时间步数的数据,如下图每个虚线方框内所示,其中X为特征数据,y为t-n+1的所有品种的收益率数据。其中l为LSTM模型输入的序列长度。
- 每个Batch包括t-n到t-1时间的虚线框内的数据。
- 这样,每个Batch的前向输入就是,所有资产在t-n到t-1每天的信号强度,这样就能计算这段时间(过去n天)组合的夏普比率的负数作为损失函数。
 原模型的其他细节
原模型的其他细节
弄清楚以上细节,对于理解本篇文章至关重要,文章具体使用的特征如下:
- 标准化后的不同时间段的每个品种的收益率,标准化的做法为区间收益率除以标准差;
- MACD指标,具体可参考原文。
原文的模型使用的是递推式滚动训练,每五年训练一次,其中前4年作为训练数据,最后1年作为验证数据。并在接下来的五年使用前五年数据训练的模型。
最终在近20年历史数据测试中,模型取得了将近3的夏普比率,具体测试结果参考原文。
趋势跟踪策略最大的问题是对于忽然转向的迟钝性,传统的量化CTA会使用多周期的方式捕捉不同时间区间的趋势收益。最近作者又在《Enhancing Time Series Momentum Strategies Using Deep Neural Networks》的基础上,针对趋势迟钝性的问题,发表了新的论文《Slow Momentum with Fast Reversion: A Trading Strategy Using Deep Learning and Changepoint Detection》。在这篇文章中,作者结合了基于高斯过程的变点检测方法(CPD),计算出每个时间点变点的得分,用于量化当前时间点作为变点的概率,再把这个CPD作为深度学习模型的特征。与原始未加入CPD的DMN模型相比,加入CPD的DMN模型的回测结果显示,最大回撤来的更低,夏普比率更高。
更多的思考
很多时候,损失函数的设计关系到模型训练优化的方向。与常用的MSE、MAE作为损失函数的时间序列预测相比,量化应用场景中,我们更应该深入这些细节。这样才能更大的发挥算法的价值。本篇文章讨论的是CTA策略的场景,将收益预测与权重预测通过一个模型得到了解决。如果是在截面多因子模型中,可以使用一个模型预测各资产的收益,另一个模型学习组合的权重,而组合权重的损失函数可以设计为夏普比率等风险收益指标。
这正如我们在前两天关于Two Sigma的文章中提到的,深度学习模型是在传统量化框架下,深入结果框架各个细节的有利提升工具。
\